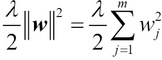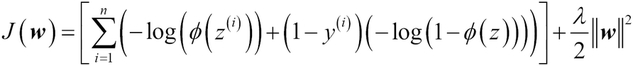Le 5 risposte
- Come risolvere l’overfitting tramite la regolarizzazione
- Come implementare una analisi kernel PCA in Python
- Quando è importante portare tutte le caratteristiche sulla stessa scala
- Come implementare un modello a regressione lineare OLS
- L’importanza delle reti neurali nel machine learning
1. Come risolvere l’overfitting tramite la regolarizzazione
L’overfitting è un problema comune nel machine learning: un modello si comporta bene sui dati di addestramento, ma non è in grado di generalizzarsi altrettanto bene su nuovi dati (dati di test).
Analogamente, il nostro modello può anche soffrire del problema opposto, underfitting (high bias, elevata discrepanza): la sua limitata complessità non è in grado di catturare lo schema presente nei dati di addestramento e pertanto soffre di scarse prestazioni anche su nuovi dati.
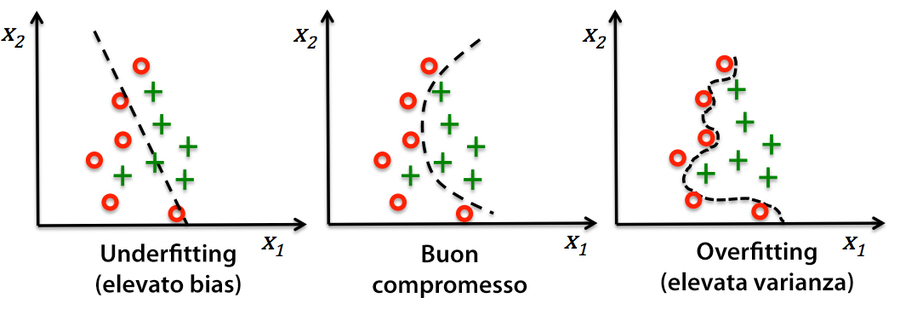
Il problema dell’overfitting e dell’underfitting può essere illustrato meglio utilizzando un confine decisionale complesso, non lineare, come nella prossima figura.
Underfitting e overfitting si contrastano meglio utilizzando un confine decisionale complesso.
Un modo per trovare un buon compromesso fra bias e varianza consiste nell’ottimizzare la complessità del modello tramite la regolarizzazione. La regolarizzazione è un metodo molto utile per gestire la colinearità (elevata correlazione fra le caratteristiche), per eliminare il rumore dai dati e prevenire l’overfitting.
Il concetto base della regolarizzazione consiste nell’introdurre informazioni aggiuntive (bias) per penalizzare i valori estremi dei parametri (pesi). La forma più comune di regolarizzazione è chiamata regolarizzazione L2 (chiamata anche riduzione L2 o riduzione dei pesi) che può essere scritta nel seguente modo:
Qui, la lettera greca lambda è il cosiddetto parametro di regolarizzazione.
La funzione di costo per la regressione logistica può essere regolarizzata aggiungendo un semplice termine di regolarizzazione, che riduce i pesi durante l’addestramento del modello:
Aggiungiamo il termine di regolarizzazione alla funzione di costo.
Tramite il parametro di regolarizzazione lambda, possiamo quindi controllare l’adattamento ai dati di addestramento contenendo l’intensità dei pesi. Incrementando il valore di lambda, incrementiamo l’intensità della regolarizzazione.
Il parametro C che è implementato per la classe LogisticRegression in scikit-learn proviene da una convenzione presente nelle macchine a vettori di supporto, argomento del prossimo paragrafo. C è direttamente correlato col parametro di regolarizzazione lambda, in quanto è il suo inverso, C = 1 / lambda.
Di conseguenza, decrementando il valore del parametro di regolarizzazione inversa C incrementiamo l’intensità della regolarizzazione, che possiamo rappresentare tracciando il percorso di regolarizzazione L2 per i due coefficienti di peso:
>>> weights, params = [], []
>>> for c in np.arange(-5, 5):
... lr = LogisticRegression(C=10**c, random_state=1,
... solver='lbfgs', multi_class='ovr')
... lr.fit(X_train_std, y_train)
... weights.append(lr.coef_[1])
... params.append(10**c)
>>> weights = np.array(weights)
>>> plt.plot(params, weights[:, 0],
... label='petal length')
>>> plt.plot(params, weights[:, 1], linestyle='--',
... label='petal width')
>>> plt.ylabel('weight coefficient')
>>> plt.xlabel('C')
>>> plt.legend(loc='upper left')
>>> plt.xscale('log')
>>> plt.show()
Tramite il codice precedente, abbiamo previsto dieci modelli a regressione logistica con valori diversi del parametro di regolarizzazione inversa C. Per scopi illustrativi, abbiamo raccolto solo i coefficienti di peso della classe 1 (qui è la seconda classe del dataset: Iris-versicolor). Ricordiamo che utilizziamo la tecnica OvR per la classificazione multiclasse.
Come possiamo vedere nel grafico risultante, i coefficienti di peso si riducono se riduciamo il parametro C, ovvero se incrementiamo l’intensità della regolarizzazione.
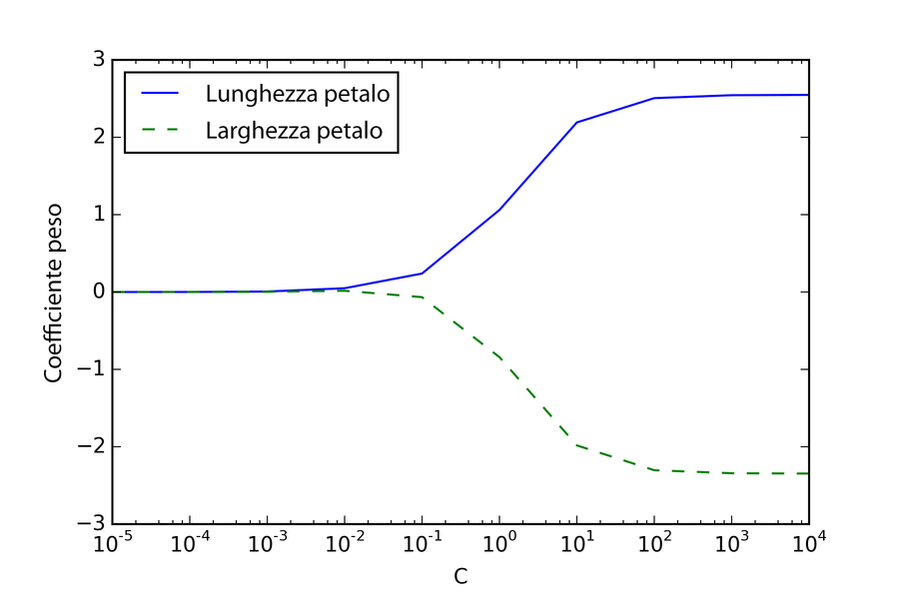
Se incrementiamo l’intensità della regolarizzazione, i coefficienti di peso si riducono.
Per sapere di più sulla regressione logistica è consigliabile la lettura del testo di Scott Menard, Logistic Regression: From Introductory to Advanced Concepts and Applications, Sage Publications, 2009.
2. Come implementare una analisi kernel PCA in Python
Utilizzando le funzioni di supporto di SciPy e NumPy, l’implementazione dell’analisi PCA kernel è in realtà molto semplice:
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF kernel PCA implementation.
Parameters
------------
X: {NumPy ndarray}, shape = [n_samples, n_features]
gamma: float
Tuning parameter of the RBF kernel
n_components: int
Number of principal components to return
Returns
------------
X_pc: {NumPy ndarray}, shape = [n_samples, k_features]
Projected dataset
"""
# Calculate pairwise squared Euclidean distances
# in the MxN dimensional dataset.
sq_dists = pdist(X, 'sqeuclidean')
# Convert pairwise distances into a square matrix.
mat_sq_dists = squareform(sq_dists)
# Compute the symmetric kernel matrix.
K = exp(-gamma * mat_sq_dists)
# Center the kernel matrix.
N = K.shape[0]
one_n = np.ones((N,N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# Obtaining eigenpairs from the centered kernel matrix
# numpy.eigh returns them in sorted order
eigvals, eigvecs = eigh(K)
# Collect the top k eigenvectors (projected samples)
X_pc = np.column_stack((eigvecs[:, -i]
for i in range(1, n_components + 1)))
return X_pc
Un difetto dell’uso dell’analisi PCA kernel RBF per la riduzione della dimensionalità è il fatto che dobbiamo specificare a priori il parametro gamma. La ricerca di un valore appropriato per gamma richiede un po’ di sperimentazione, che può essere svolta al meglio utilizzando algoritmi di ottimizzazione del parametro, per esempio la ricerca a griglia.
Esempio: separazione di forme a mezzaluna
Ora applichiamo rbf_kernel_pca su alcuni dataset d’esempio non lineari. Inizieremo creando un dataset bidimensionale di 100 punti campione che producono due forme a mezzaluna:
>>> from sklearn.datasets import make_moons >>> X, y = make_moons(n_samples=100, random_state=123) >>> plt.scatter(X[y==0, 0], X[y==0, 1], ... color='red', marker='^', alpha=0.5) >>> plt.scatter(X[y==1, 0], X[y==1, 1], ... color='blue', marker='o', alpha=0.5) >>> plt.show()
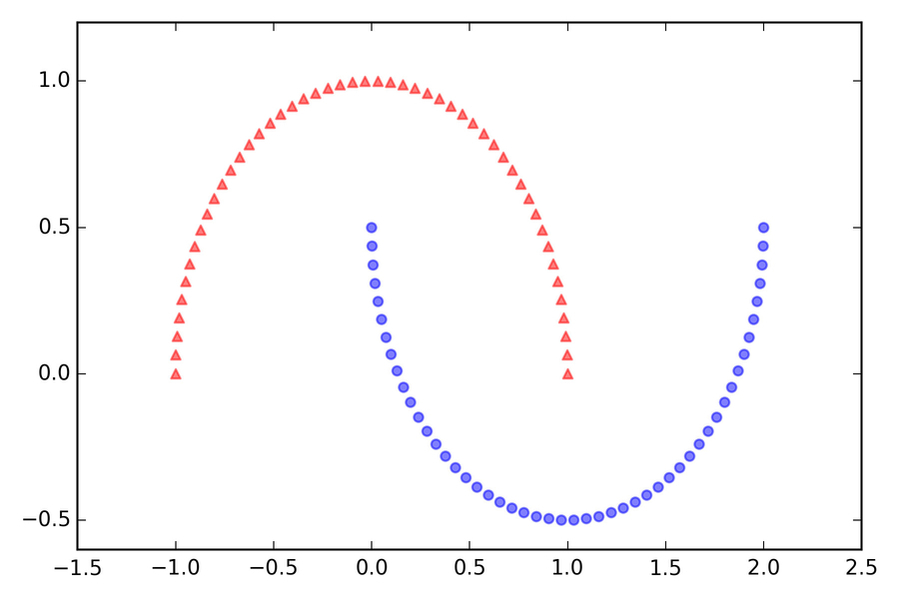
Per gli scopi dell’illustrazione, la mezzaluna dei simboli triangolari rappresenterà una classe e la mezzaluna dei simboli circolari rappresenterà i campioni dell’altra classe (nella figura che segue).
Due forme a mezzaluna.
Con ogni evidenza, queste due forme a mezzaluna non sono separabili linearmente e il nostro obiettivo è quello di “dispiegare” le mezzelune con un’analisi a kernel dei com- ponenti principali, KPCA, in modo che il dataset possa diventare un input adatto per un classificatore lineare. Ma innanzitutto, vediamo l’aspetto del dataset se lo proiettiamo sui componenti principali con una PCA standard:
>>> from sklearn.decomposition import PCA
>>> scikit_pca = PCA(n_components=2)
>>> X_spca = scikit_pca.fit_transform(X)
>>> fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
... color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
... color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_spca[y==0, 0], np.zeros((50,1))+0.02,
... color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_spca[y==1, 0], np.zeros((50,1))-0.02,
... color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()
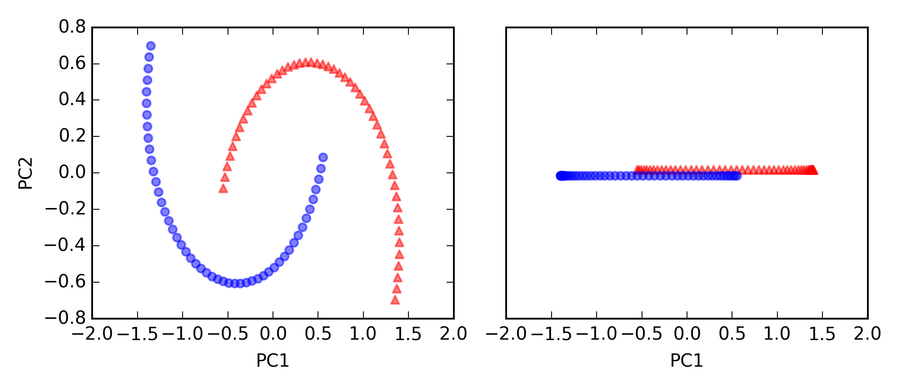
Chiaramente, possiamo vedere nella figura risultante che un classificatore lineare non sarebbe assolutamente in grado di comportarsi correttamente sul dataset trasformato tramite un’analisi PCA standard.
Si noti che nel tracciato del solo primo componente principale (grafico a destra), abbiamo alzato leggermente i campioni triangolari e abbassato leggermente i campioni circolari, con il solo scopo di visualizzarli, altrimenti i campioni si sarebbero sovrapposti.
Un classificatore lineare non funzionerebbe.
Ora, tentiamo di utilizzare la funzione PCA kernel rbf_kernel_pca, che abbiamo implementato nel paragrafo precedente:
>>> X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
>>> fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
... color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
... color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==0, 0], np.zeros((50,1))+0.02,
... color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==1, 0], np.zeros((50,1))-0.02,
... color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()
Possiamo vedere che le due classi (cerchi e triangoli) ora sono separabili linearmente e dunque il dataset di addestramento diviene adatto all’impiego di un classificatore lineare.
Sfortunatamente non esiste alcun valore universale del parametro di ottimizzazione gamma che funzioni al meglio con dataset differenti. Per trovare un valore gamma che sia appropriato per un determinato problema è necessario sperimentare.
3. Quando è importante portare tutte le caratteristiche sulla stessa scala
La scala delle caratteristiche è un elemento fondamentale nella catena di pre-elaborazione e di cui è facile dimenticarsi. Gli alberi decisionali nelle foreste casuali sono fra i pochi algoritmi di machine learning in cui non dobbiamo preoccuparci della scala delle caratteristiche. Tuttavia, la maggior parte degli algoritmi di machine learning e di ottimizzazione si comporta molto meglio se le caratteristiche adottano la stessa scala.
L’importanza della riduzione in scala delle caratteristiche può essere illustrata da un semplice esempio. Supponiamo di avere due caratteristiche, nelle quali una è misurata su una scala da 1 a 10 e la seconda è misurata su una scala da 1 a 100.000. Quando consideriamo la funzione di errore al quadrato di Adaline, è facile capire che l’algoritmo sarà occupato principalmente a ottimizzare i pesi sulla base degli errori offerti dalla seconda caratteristica. Un altro esempio è l’algoritmo kNN (k-nearest neighbors) con una misurazione della distanza euclidea; le distanze calcolate fra campioni saranno premiate dal secondo asse, ovvero dalla seconda caratteristica.
Ora, vi sono due approcci per portare caratteristiche differenti sulla stessa scala: la normalizzazione e la standardizzazione. Questi termini vengono frequentemente utilizzati in modo piuttosto vago in vari campi e il loro significato deve essere derivato dal contesto. In generale, la normalizzazione fa riferimento al cambiamento di scala della caratteristica in un intervallo [0, 1], che è un caso speciale di riduzione in scala min-max. Per normalizzare i dati, applichiamo semplicemente la scala min-max a ciascuna colonna delle caratteristiche, dove il nuovo valore di un campione può essere calcolato considerano un particolare campione, il più piccolo valore nella colonna della caratteristica e il valore più grande.
La procedura di riduzione in scala min-max è implementata in scikit-learn e può essere utilizzata nel seguente modo:
>>> from sklearn.preprocessing import MinMaxScaler >>> mms = MinMaxScaler() >>> X_train_norm = mms.fit_transform(X_train) >>> X_test_norm = mms.transform(X_test)
Sebbene la normalizzazione in scala min-max sia una tecnica comunemente utilizzata che risulta utile quando occorre mantenere i valori in un intervallo ben definito, la standardizzazione può essere più pratica per molti algoritmi di machine learning. Il motivo è che molti modelli lineari, come la regressione logistica e la SVM, inizializzano i pesi a 0 o a piccoli valori casuali prossimi a 0.
Utilizzando la standardizzazione, centriamo la colonna della caratteristica alla media 0 con deviazione standard 1, in modo che la colonna della caratteristica assuma la forma di una distribuzione normale, dalla quale è più facile derivare i pesi. Inoltre, la standardizzazione mantiene informazioni utili riguardo alle anomalie e rende l’algoritmo meno sensibile a questo problema rispetto alla riduzione in scala min-max, che riporta i dati a un intervallo limitato di valori.
La procedura di standardizzazione può essere espressa dalla seguente equazione:
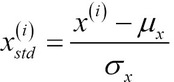
Qui, ![]() è la media del campione di una determinata colonna di caratteristiche e
è la media del campione di una determinata colonna di caratteristiche e ![]() è la corrispondente deviazione standard.
è la corrispondente deviazione standard.
La seguente tabella illustra la differenza esistente fra le due tecniche più comunemente utilizzate di riduzione in scala delle caratteristiche, di standardizzazione e di normalizzazione su un semplice dataset campione costituito dai numeri compresi tra 0 e 5:
| Input | Standardizzazione | Normalizzazione |
|---|---|---|
| 0.0 | -1.336306 | 0.0 |
| 1.0 | -0.801784 | 0.2 |
| 2.0 | -0.267261 | 0.4 |
| 3.0 | 0.267261 | 0.6 |
| 4.0 | 0.801784 | 0.8 |
| 5.0 | 1.336306 | 1.0 |
Analogamente a MinMaxScaler, scikit-learn implementa anche una classe per la standardizzazione:
>>> from sklearn.preprocessing import StandardScaler >>> stdsc = StandardScaler() >>> X_train_std = stdsc.fit_transform(X_train) >>> X_test_std = stdsc.transform(X_test)
Di nuovo, è importante anche evidenziare il fatto che adattiamo StandardScaler una prima volta sui dati di addestramento e poi utilizziamo questi stessi parametri per trasformare il set di test o ogni nuovo punto dei dati.
4. Come implementare un modello a regressione lineare OLS
La regressione lineare può essere considerata come la ricerca della linea retta migliore che attraversa i punti campione dei dati di addestramento. Tuttavia, non abbiamo né definito il termine migliore, né abbiamo trattato le varie tecniche di adattamento di tale modello. Nei prossimi paragrafi riempiremo le tessere mancanti di questo puzzle, utilizzando il metodo OLS (Ordinary Least Squares) per stimare i parametri della linea di regressione che minimizza la somma delle distanze verticali al quadrato (i residui o gli errori) nei punti di campionamento.
Risoluzione dei parametri di regressione nella discesa del gradiente
Ricordiamo che il neurone artificiale utilizza una funzione di attivazione lineare e che occorre definire una funzione di costo da minimizzare per apprendere i pesi tramite degli algoritmi di ottimizzazione, come Gradient Descent (GD) e Stochastic Gradient Descent (SGD). Questa funzione di costo in Adaline si chiama Sum of Squared Errors (SSE). È identica alla funzione di costo OLS che abbiamo definito:
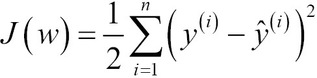
Sostanzialmente, la regressione lineare OLS può essere considerata come un Adaline senza la funzione del passo unitario, in modo che possiamo ottenere valori target continui, invece che etichette delle sole classi -1 e 1. Per illustrare questa analogia, prendiamo l’implementazione a discesa del gradiente (GD) ed eliminiamo la funzione del passo unitario per implementare il nostro primo modello a regressione lineare:
class LinearRegressionGD(object):
def __init__(self, eta=0.001, n_iter=20):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return self.net_input(X)
Per vedere in azione il nostro regressore LinearRegressionGD, utilizzeremo la variabile RM (numero di stanze) del dataset Housing quale variabile descrittiva per addestrare un modello che sia in grado di prevedere MEDV (il prezzo delle case). Inoltre, standardizzeremo le variabili per ottenere una migliore convergenza dell’algoritmo a discesa del gradiente. Il codice è il seguente:
>>> X = df[['RM']].values >>> y = df['MEDV'].values >>> from sklearn.preprocessing import StandardScaler >>> sc_x = StandardScaler() >>> sc_y = StandardScaler() >>> X_std = sc_x.fit_transform(X) >>> y_std = sc_y.fit_transform(y) >>> lr = LinearRegressionGD() >>> lr.fit(X_std, y_std)
Quando utilizziamo gli algoritmi di ottimizzazione, come la discesa del gradiente, è sempre una buona idea tracciare il costo come una funzione del numero di epoch (passi di addestramento), con lo scopo di verificarne la convergenza. In sintesi, tracciamo il costo rispetto al numero di epoch, per controllare se la regressione lineare converge:
>>> plt.plot(range(1, lr.n_iter+1), lr.cost_)
>>> plt.ylabel('SSE')
>>> plt.xlabel('Epoch')
>>> plt.show()
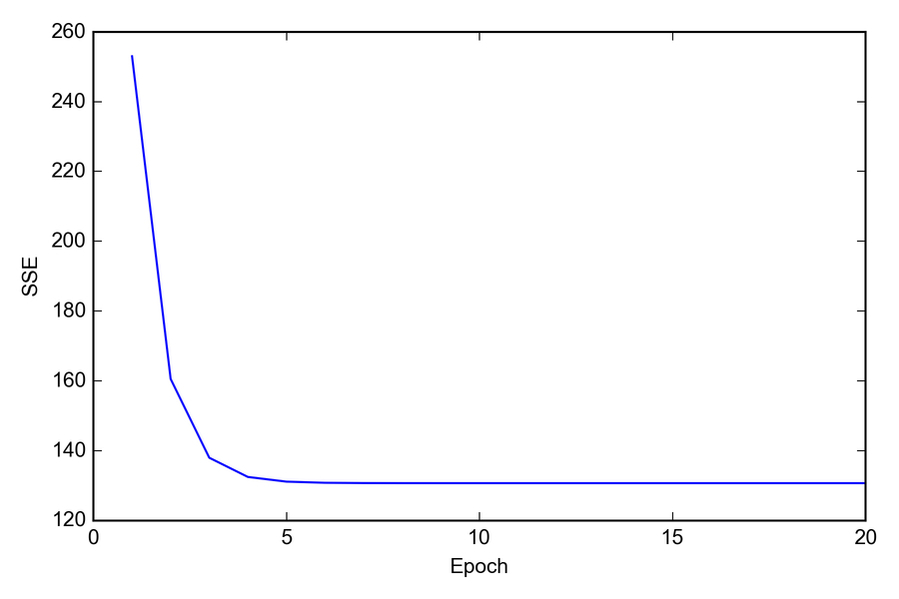
Come possiamo vedere nel grafico rappresentato nella figura, l’algoritmo GD inizia a convergere dopo la quinta epoch.
Convergenza dell’algoritmo GD dopo la quinta epoch.
Ora, visualizziamo la qualità con cui la linea della regressione lineare attraversa i dati di addestramento. Per farlo, definiremo una semplice funzione di supporto che traccerà un grafico a dispersione dei campioni di addestramento e aggiungerà la linea di regressione:
>>> def lin_regplot(X, y, model): ... plt.scatter(X, y, c='blue') ... plt.plot(X, model.predict(X), color='red') ... return None
Ora utilizzeremo la funzione lin_regplot per tracciare il numero di stanze rispetto al prezzo delle abitazioni:
>>> lin_regplot(X_std, y_std, lr)
>>> plt.xlabel('Average number of rooms [RM] (standardized)')
>>> plt.ylabel('Price in $1000\'s [MEDV] (standardized)')
>>> plt.show()
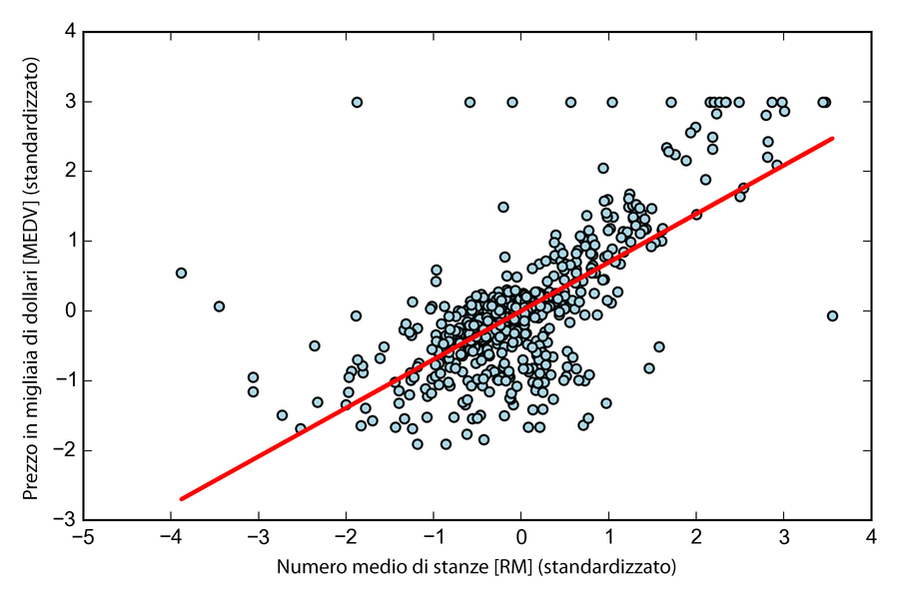
Come possiamo vedere nella prossima figura, la linea di regressione lineare riflette la tendenza generale, ovvero il fatto che il prezzo delle abitazioni tende ad aumentare con il numero delle stanze.
Il prezzo delle abitazioni tende ad aumentare con il numero delle stanze.
Sebbene questa osservazione abbia un senso anche dal punto di vista intuitivo, i dati ci dicono anche che il numero delle stanze non spiega appieno il prezzo delle abitazioni. È interessante notare che possiamo anche osservare una curiosa linea su y=3 che suggerisce il fatto che i prezzi possono essere stati troncati. In alcune applicazioni, può anche essere importante rilevare le variabili previste nella loro scala originaria. Per calcolare la scala del prezzo risultante riportandolo sull’asse dei prezzi in migliaia di dollari, possiamo semplicemente aggiungere a StandardScaler il metodo inverse_transform:
>>> num_rooms_std = sc_x.transform([5.0])
>>> price_std = lr.predict(num_rooms_std)
>>> print("Price in $1000's: %.3f" % \
... sc_y.inverse_transform(price_std))
Price in $1000's: 10.840
Nel precedente esempio di codice, abbiamo utilizzato il modello a regressione lineare precedentemente addestrato per prevedere il prezzo di un’abitazione di cinque stanze. Secondo il nostro modello, tale abitazione dovrebbe valere $10.840.
A margine, vale anche la pena di menzionare che, tecnicamente, non siamo costretti ad aggiornare i pesi dell’intercettazione se stiamo lavorando su variabili standardizzate, in quanto in questi casi l’asse y viene intercettato sempre a 0. Possiamo confermarlo rapidamente stampando i pesi:
>>> print('Slope: %.3f' % lr.w_[1])
Slope: 0.695
>>> print('Intercept: %.3f' % lr.w_[0])
Intercept: -0.000
Stima del coefficiente di un modello regressione lineare tramite scikit-learn
Nel paragrafo precedente, abbiamo implementato un modello funzionante di analisi a regressione. Tuttavia, in un’applicazione reale, potremmo essere interessati a implementazioni più efficienti; per esempio, l’oggetto LinearRegression di scikit-learn che utilizza la libreria LIBLINEAR è un algoritmo di ottimizzazione avanzato che funzionano meglio con variabili non standardizzate. Questo può essere un vantaggio per alcune applicazioni:
>>> from sklearn.linear_model import LinearRegression
>>> slr = LinearRegression()
>>> slr.fit(X, y)
>>> print('Slope: %.3f' % slr.coef_[0])
Slope: 9.102
>>> print('Intercept: %.3f' % slr.intercept_)
Intercept: -34.671
Come possiamo vedere eseguendo il codice precedente, il modello LinearRegression di scikit-learn adattato con le variabili RM e MEDV non standardizzate ha fornito coefficienti differenti. Confrontiamolo con la nostra implementazione a discesa del gradiente, tracciando MEDV rispetto a RM:
>>> lin_regplot(X, y, slr)
>>> plt.xlabel('Average number of rooms [RM]')
>>> plt.ylabel('Price in $1000\'s [MEDV]')
>>> plt.show()w
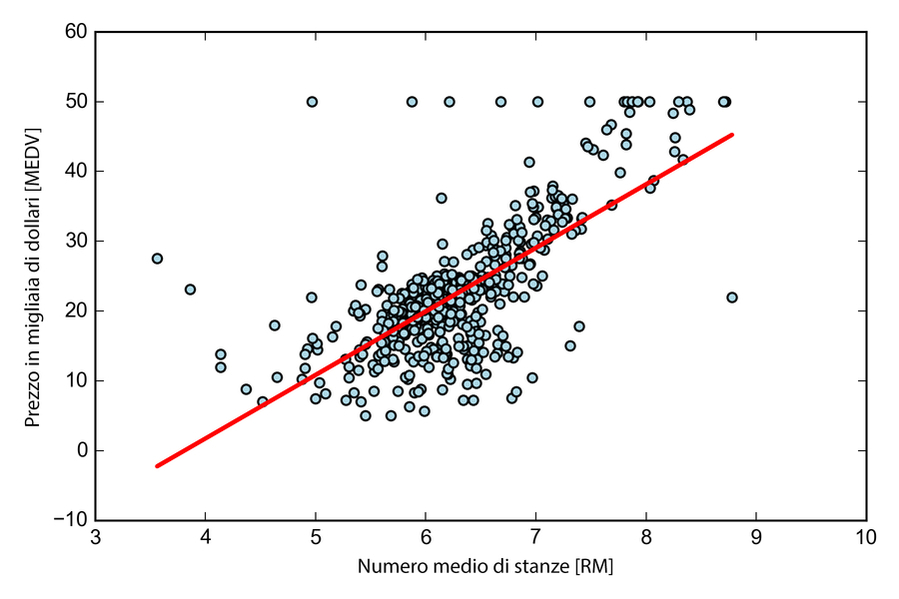
Ora, quando tracciamo i dati di addestramento e il nostro modello adattato tramite il codice precedente, possiamo vedere (nella figura seguente) che il risultato generale sembra identico alla nostra implementazione a discesa del gradiente.
Dati di addestramento e modello adattato.
5. L’importanza delle reti neurali nel machine learning
Il deep learning è un argomento sempre più dibattuto ed è, senza alcun dubbio, l’argomento più affascinante nel campo del machine learning. Il deep learning può essere considerato come un insieme di algoritmi che sono stati sviluppati per addestrare con particolare efficienza reti neurali artificiali composte da più livelli.
Modellare funzioni complesse con reti neurali artificiali
I neuroni artificiali rappresentano gli elementi costitutivi delle reti neurali artificiali multilivello. Il concetto su cui si basano le reti neurali artificiali deriva da ipotesi e modelli del funzionamento del cervello umano, quando si trova a dover risolvere problemi complessi.
Sebbene le reti neurali artificiali abbiano acquisito una grande popolarità nel corso degli ultimi anni, i primi studi in questo senso risalgono agli anni Quaranta, quando Warren McCulloch e Walter Pitt descrissero il funzionamento dei neuroni. Tuttavia, nei decenni che seguirono la prima implementazione del modello del neurone di McCulloch-Pitt, ovvero il perceptron di Rosenblatt, negli anni Cinquanta, molti ricercatori ed esperti di machine learning iniziarono lentamente a perdere interesse nelle reti neurali, in quanto nessuno aveva una buona soluzione per l’addestramento di una rete neurale multilivello.
Alla fine, l’interesse nei confronti delle reti neurali si è ravvivato nel 1986, quando D.E. Rumelhart, G.E. Hinton e R.J. Williams furono coinvolti nella riscoperta e diffusione dell’algoritmo di retropropagazione (backpropagation) per addestrare in modo più efficiente le reti neurali (David E. Rumelhart, Geoffrey E. Hinton, Ronald J. Williams (1986), Learning Representations by Back-propagating Errors, in Nature 323 (6088): 533–536).
Nel corso del decennio precedente, vi sono state molte grandi scoperte nel campo degli algoritmi che oggi chiamiamo di feature detector, che possono essere utilizzati per creare rilevatori di caratteristiche a partire da dati senza etichetta, in modo da pre-addestrare le reti neurali profonde, ovvero costituite da più livelli.
Dall’accademia al web
Le reti neurali sono un argomento interessante non solo in ambito accademico, ma anche per grandi utilizzatori di tecnologie come Facebook, Microsoft e Google, i quali investono pesantemente nelle reti neurali artificiali e nella ricerca nell’ambito del deep learning. Al momento attuale, le reti neurali complesse, alimentate dagli algoritmi di deep learning, sono considerate lo stato dell’arte nella soluzione dei problemi complessi come il riconoscimento delle immagini e del parlato.
Fra gli esempi più noti di prodotti della vita quotidiana che funzionano grazie al deep learning vi sono la ricerca per immagini di Google e anche Google Translate, un’applicazione per smartphone in grado di riconoscere automaticamente il testo nelle immagini ed eseguire una traduzione in tempo reale in venti diverse lingue.
Ma molte altre e interessanti applicazioni delle reti neurali profonde sono attualmente in fase di sviluppo presso le principali società che si occupano di alte tecnologie, per esempio DeepFace di Facebook per il tagging delle immagini (Y. Taigman, M. Yang, M. Ranzato e L. Wolf, DeepFace: Closing the gap to human-level performance in face verification, in Computer Vision and Pattern Recognition CVPR, 2014 IEEE Conference, pp. 1701–1708) e DeepSpeech di Baidu, che è in grado di gestire le richieste vocali in lingua mandarina (A. Hannun, C. Case, J. Casper, B. Catanzaro, G. Diamos, E. Elsen, R. Prenger, S. Satheesh, S. Sengupta, A. Coates, et al. DeepSpeech: Scaling up end-to-end speech recognition, arXiv preprint arXiv:1412.5567, 2014). Inoltre, l’industria farmaceutica ha recentemente iniziato a utilizzare tecniche di deep learning per la scelta dei principi attivi e per la previsione della tossicità e la ricerca ha dimostrato che queste nuove tecniche superano notevolmente le prestazioni dei metodi tradizionali di screening virtuale (T. Unterthiner, A. Mayr, G. Klambauer e S. Hochreiter, Toxicity prediction using deep learning, arXiv preprint arXiv:1503.01445, 2015).
Questo articolo richiama contenuti da Machine Learning con Python e Machine Learning con Python – nuova edizione.
L'autore
Corsi che potrebbero interessarti
Data governance: diritti, licenze e privacy
Agile, sviluppo e management: iniziare bene
Big Data Executive: business e strategie