La regressione permette di formulare previsioni basate sui dati
Le relazioni matematiche ci aiutano a spiegare molti aspetti della nostra vita quotidiana. Per esempio, il peso corporeo è funzione delle calorie assunte; spesso il reddito è correlato al livello di istruzione e all’esperienza professionale; e i sondaggi aiutano a stimare le possibilità di rielezione di un presidente.
Quando tali schemi sono formulati tramite numeri, le cose divengono ancora più chiare. Per esempio, un aumento di 250 kilocalorie assunte quotidianamente, porta a un aumento del peso corporeo di circa un chilogrammo al mese; ogni anno di esperienza di lavoro può valere un aumento di 1.000 euro; e un presidente ha più probabilità di essere rieletto se l’economia va forte. Ovviamente, queste equazioni non sono perfettamente adatte a ogni situazione, ma ci aspettiamo che siano ragionevolmente corrette nella maggior parte dei casi.
Che cos’è la regressione
L’origine del termine regressione per descrivere il processo di configurazione di determinate linee ai dati deriva da uno studio sulla genetica di Sir Francis Galton alla fine del XIX secolo. Egli scoprì che i padri che erano estremamente bassi o alti di statura tendevano ad avere figli la cui statura era più vicina alla media della popolazione. Chiamò questo fenomeno regressione alla media.
La regressione prevede la determinazione della relazione fra un’unica variabile numerica dipendente (il valore da predire) e una o più variabili numeriche indipendenti (i predittori). Come specifica anche il suo nome, la variabile dipendente dipende dal valore della o delle variabili indipendenti. Le forme più semplici della regressione partono dal presupposto che la relazione fra la o le variabili indipendenti e la variabile dipendente segua una linea retta.
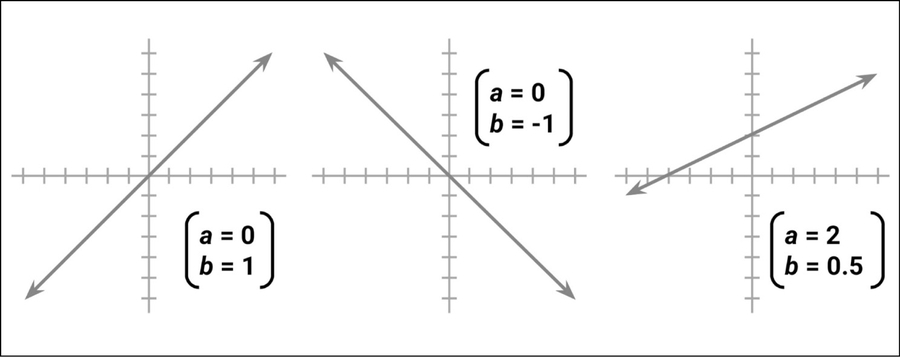
Ricorderemo forse, dalle lezioni di algebra, che le linee possono essere definite da una formula a pendenza e intercettazione: y = a + bx. In questa forma, la lettera y indica la variabile dipendente e la lettera x indica la variabile indipendente. Il termine della pendenza b specifica quanto cresce la linea a ogni incremento di x. Valori positivi definiscono linee crescenti mentre valori negativi definiscono linee calanti. Il termine a è l’intercettazione, in quanto specifica il punto in cui la linea attraversa o intercetta, l’asse verticale y. Esso indica il valore di y quando x = 0.
Esempi di linee con varie pendenze e intercettazioni.
Le equazioni di regressione modellano i dati impiegando un formato simile, a pendenza e intercettazione. Il compito della macchina consiste nell’identificare i valori di a e b tali per cui la linea specificata è la più efficace nel correlare i valori di x ai valori di y. Non sempre esiste un’unica funzione in grado di correlare perfettamente i valori, pertanto la macchina deve anche avere un modo per quantificare il margine d’errore.
Usi della regressione
L’analisi a regressione viene utilizzata per un’ampia varietà di compiti: è quasi sicuramente il metodo di machine learning più utilizzato. Può essere impiegato sia per spiegare il passato sia per estrapolare il futuro e può essere applicato a praticamente ogni compito. Ecco alcuni casi specifici d’uso.
- Esaminare come le popolazioni e gli individui variano in termini di caratteristiche misurabili, nell’ambito di studi scientifici nei campi dell’economia, della sociologia, della psicologia, della fisica e dell’ecologia.
- Quantificare la relazione di causa fra un evento e la sua reazione, in casi come i test di nuove cure, i test ingegneristici sulla sicurezza o le ricerche di marketing.
- Identificare degli schemi, per prevedere i comportamenti futuri sulla base di determinati criteri noti, nei campi assicurativo, dei disastri naturali, elettorale e criminale.
I metodi a regressione sono impiegati anche per la verifica delle ipotesi statistiche, ovvero per determinare se una premessa ha più probabilità di essere vera o falsa alla luce dei dati osservati. Le stime del modello a regressione della forza e coerenza di una relazione forniscono informazioni che possono essere impiegate per valutare se le osservazioni sono dovute al puro caso.
(La verifica delle ipotesi è un argomento estremamente dettagliato e non rientra negli scopi del machine learning. Chi avesse un interesse per questo argomento potrebbe partire da un libro di testo introduttivo alla statistica. Per esempio Intuitive Introductory Statistics, Wolfe, D.A. e Schneider, G., Springer, 2017).
L’analisi a regressione non si esplicita con un unico algoritmo. Piuttosto, si tratta di un termine generico per una grande quantità di metodi che possono essere adattati a quasi ogni compito di machine learning. Se dovessimo scegliere un unico metodo di machine learning da studiare, la regressione sarebbe una buona scelta. Si potrebbe dedicare un’intera carriera a questo argomento e probabilmente rimarrebbe ancora qualcosa da imparare.
La regressione può essere utilizzata anche per altri tipi di variabili dipendenti e perfino per alcuni compiti di classificazione. Per esempio, la regressione logistica viene utilizzata per modellare un risultato categorico binario, mentre la regressione di Poisson, che trae il suo nome dal matematico francese Siméon Poisson, modella il conteggio di dati interi. Il metodo di regressione logistica multinomiale modella un risultato categorico e pertanto può essere utilizzata per scopi di classificazione. Poiché a tutti i metodi a regressione si applicano gli stessi principi statistici, dopo aver compreso il caso lineare, le altre varianti saranno più facilmente comprensibili.
Molti dei metodi a regressione più specializzati rientrano nella classe detta GLM (Generalized Linear Models). Impiegando un modello GLM, i modelli lineari possono essere generalizzati ad altri schemi tramite l’impiego di una funzione di collegamento, che specifica relazioni più complesse fra x e y. Questo consente di applicare la regressione a quasi ogni tipo di dati.
Vediamo ora il caso base della regressione lineare semplice. Nonostante il nome, questo metodo non è affatto semplice nella sua capacità di risolvere problemi complessi. Più avanti scopriremo come l’utilizzo di un modello a regressione lineare semplice avrebbe potuto evitare un tragico disastro dell’ingegneria.
La regressione lineare semplice
Il 28 gennaio del 1986, sette membri dell’equipaggio dello Space Shuttle Challenger perirono a causa di un guasto a un booster, che ha causato la catastrofica disintegrazione della navicella. Nelle successive indagini, gli esperti si concentrarono rapidamente sulla temperatura al lancio quale potenziale responsabile del problema. Le guarnizioni o-ring responsabili della tenuta dei giunti del missile non erano mai state collaudate sotto i 4°C (ovvero 40°F) e le condizioni meteorologiche al lancio erano insolitamente rigide e sotto il punto di congelamento.
Col senno di poi, l’incidente è diventato un caso di studio per l’importanza dell’analisi e della rappresentazione dei dati. Sebbene non sia chiaro quali informazioni fossero disponibili agli ingegneri missilistici e ai responsabili prima del lancio, è innegabile che la disponibilità di dati migliori, utilizzati con attenzione, avrebbe potuto sventare questo disastro.
L’analisi trattata in questo paragrafo si basa sui dati presentati in Risk Analysis of the Space Shuttle: Pre-Challenger Prediction of Failure, Dalal S.R., Fowlkes E.B. e Hoadley B., in Journal of the American Statistical Association, 1989, Vol. 84, pp. 945-957. Per una prospettiva sul modo in cui i dati avrebbero potuto cambiare il corso degli eventi, consultiamo Visual Explanations: Images and Quantities, Evidence and Narrative, Tufte, E.R., Cheshire, C.T.: Graphics Press, 1997. Per un contrappunto, leggiamo Representation and misrepresentation: Tufte and the Morton Thiokol engineers on the Challenger, Robison, W., Boisjoly, R., Hoeker, D. e Young, S., in “Science e Engineering Ethics”, 2002, Vol. 8, pp. 59-81.
Gli ingegneri missilistici quasi certamente sapevano che le temperature rigide potevano alterare la tenuta dei componenti e pregiudicare la loro capacità di svolgere la loro funzione sigillante, cosa che avrebbe aumentato le probabilità che si producesse una pericolosa perdita di combustibile. Tuttavia, a causa delle pressioni politiche a procedere con il lancio, avevano bisogno di opporre dei dati a supporto di questa ipotesi. Un modello a regressione che dimostrasse un legame fra temperature e guasti agli o-ring e potesse prevedere la possibilità di un guasto in base alle temperature previste al lancio, sarebbe stato molto utile.
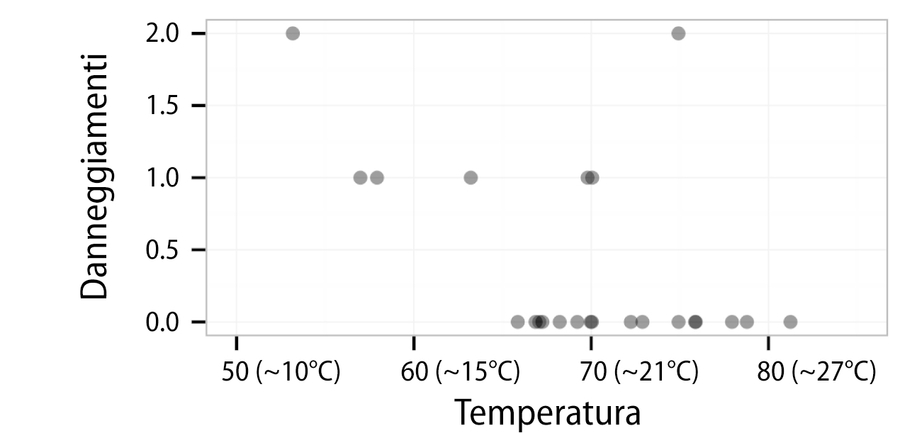
Per costruire il modello a regressione, gli scienziati avrebbero dovuto utilizzare i dati delle temperature al lancio e dei danneggiamenti ai componenti registrati durante le 23 missioni precedenti dello shuttle. Un danneggiamento ai componenti può indicare due tipi di problemi. Il primo, l’erosione, si verifica quando un calore eccessivo brucia l’o-ring. Il secondo problema, di decompressione, si verifica quando dei gas caldi sfuggono a un o-ring che ha perso la capacità sigillante. Poiché lo shuttle aveva un totale di sei o-ring primari, a ogni lancio occorreva controllare sei possibili danneggiamenti. Sebbene il velivolo potesse resistere a uno o più danneggiamenti o venire distrutto da uno solo di essi, ogni ulteriore danneggiamento incrementava la probabilità di un guasto catastrofico. Il grafico di dispersione della prossima figura presenta i danneggiamenti agli o-ring primari rilevati nei precedenti 23 lanci, relativamente alla temperatura al lancio.
Una rappresentazione dei danneggiamenti agli o-ring dello space shuttle rispetto alla temperatura al lancio.
Esaminando il grafico, si nota una tendenza evidente: i lanci con temperature più elevate tendono ad avere meno eventi di danneggiamento degli o-ring. Inoltre, il lancio con temperature più rigide (53°F, ovvero circa 12°C) aveva manifestato ben due eventi, un livello raggiunto solo in un altro lancio. Sulla base di questa informazione, il fatto che il lancio del Challenger fosse programmato in condizioni ben più rigide (-0,5°C) doveva suscitare preoccupazioni. Ma, esattamente, quali dovevano essere quelle preoccupazioni? Per rispondere a questa domanda, possiamo ricorrere alla regressione lineare semplice.
Un modello a regressione lineare semplice definisce la relazione fra una variabile dipendente e un’unica variabile predittrice indipendente, impiegando una linea definita da un’equazione nella seguente forma:
A parte le lettere greche, questa equazione è praticamente identica alla forma pendenza-intercettazione descritta precedentemente. L’intercettazione, α (alfa), descrive il punto in cui la linea attraversa l’asse delle y, mentre la pendenza, β (beta), descrive la variazione in y data da un incremento in x. Per i dati di lancio dello shuttle, la pendenza ci dice la variazione prevista nel tasso di guasti agli o-ring per ogni variazione della temperatura al lancio.
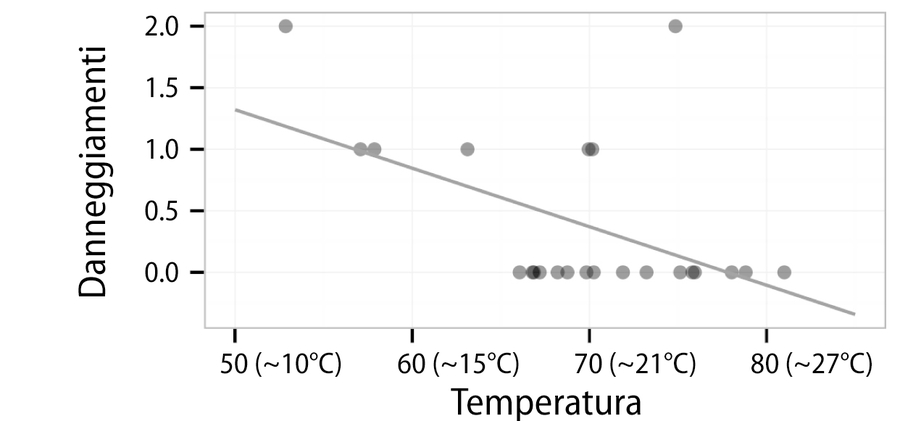
Supponiamo di sapere che i parametri stimati dalla regressione nell’equazione per i dati di lancio dello shuttle siano a = 3,70 e b = -0,048. Di conseguenza, l’equazione lineare completa è y = 3,70 – 0,048x. Ignorando per un momento il modo in cui sono stati ottenuti questi numeri, possiamo tracciare sul grafico di dispersione la linea rappresentata nella figura sottostante.
Una linea di regressione che modella la relazione fra gli eventi di danneggiamento e la temperatura al lancio.
Come mostra la linea, a 60°F (circa 15°C) prediciamo meno di un danneggiamento agli o-ring. A 50°F (circa 10°C), ci aspettiamo di avere 1,3 danneggiamenti. Se impieghiamo il modello per estrapolare il valore a 31°F (-0,5°C), la temperatura prevista al lancio del Challenger, ci aspetteremmo circa 3,70 – 0,048 ∗ 31 = 2,21 eventi di danneggiamento degli o-ring.
Supponendo che ogni guasto agli o-ring aumenti di ugual misura la probabilità di una fuga catastrofica di carburante, questo significa che il lancio del Challenger a quella temperatura sotto zero era circa tre volte più pericolosa di un tipico lancio a 15°C e oltre otto volte più pericolosa di un lancio a 21°C.
Notiamo che la linea non passa esattamente attraverso ogni punto dei dati. Al contrario, suddivide i dati abbastanza equamente, e alcuni dati sono situati sotto o sopra tale linea. In un prossimo paragrafo, scopriremo come è stata scelta questa specifica linea.
Questo articolo richiama contenuti dal capitolo 6 di Machine Learning con R.
Immagine di apertura di Michael Dziedzic su Unsplash.