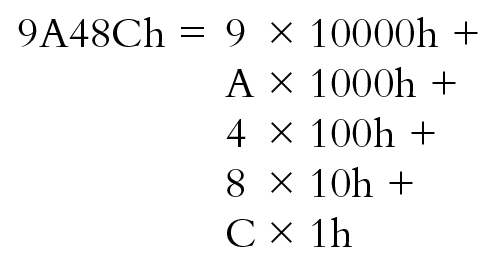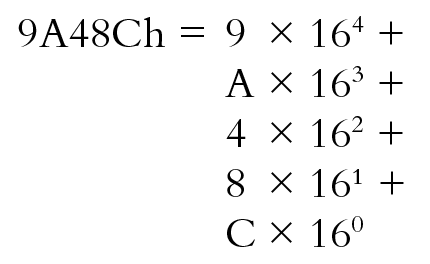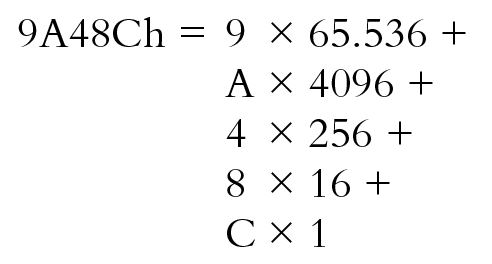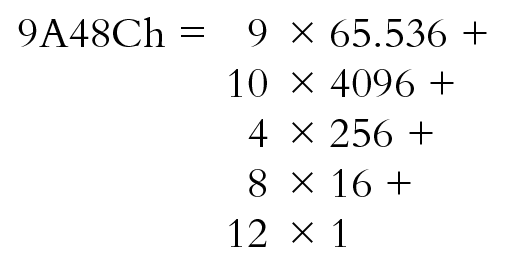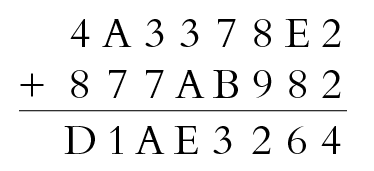Il codice esadecimale è ideale per maneggiare le parole del computer
Singoli bit possono fare affermazioni importanti: sì o no, vero o falso, test superato o fallito. Molto più spesso, però, si raggruppano fra loro più bit per rappresentare numeri e, da lì, ogni tipo di dati, come testo, suoni, musica, immagini, filmati. Un circuito che somma due bit è interessante, ma uno che sommi più bit – come, vedremo, si fa in codice esadecimale – è sulla strada giusta per diventare parte di un vero computer.
Per comodità di spostamento e manipolazione, i computer spesso raggruppano un certo numero di bit in una entità chiamata parola (word). La lunghezza della parola (cioè il numero di bit che la compongono) è fondamentale per l’architettura del computer, perché tutti i dati di quel computer si spostano in gruppi di una parola o di multipli della parola.
Alcuni fra i primi computer usavano parole di lunghezze multiple di 6 bit, come 12, 18, 24 bit. Erano comode per il semplice motivo che i valori sono rappresentati facilmente con i numeri ottali.
Numeri in binario e in ottale
| Binario | Ottale |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Una parola di 6 bit può essere rappresentata precisamente da due cifre ottali e le parole con le dimensioni di 12, 18 e 24 bit sono semplicemente dei multipli: una parola di 24 bit richiede otto cifre ottali.
L’industria dei computer però è andata in una direzione leggermente diversa. Una volta riconosciuta l’importanza dei numeri binari, deve essere sembrato quasi perverso lavorare con parole di dimensioni come 6, 12, 18 o 24, che non sono potenze di due e sono invece multipli di tre.
A questo punto arriva il byte.
La parola byte ha avuto origine in IBM, probabilmente intorno al 1956: deriva da bite (boccone), ma scritta con la y in modo da non fare confusione con bit. Inizialmente, un byte indicava semplicemente il numero dei bit in un particolare percorso di dati, ma verso la metà degli anni Sessanta, parallelamente allo sviluppo di una grande serie di computer commerciali denominati System/360, la parola byte ha iniziato a significare un gruppo di 8 bit.
Il significato è rimasto: gli 8 bit che costituiscono un byte sono ora una misura universale dei dati digitali.
Dato che è costituito da 8 bit, un byte può assumere i valori da 00000000 a 11111111, che possono rappresentare i numeri decimali da 0 a 255, ovvero una su 28, cioè 256, cose diverse.
Si dà il caso che 8 sia un buon numero di bit, non troppo piccolo e non troppo grande. Il byte è giusto, in più di un modo. È ideale per memorizzare il testo, perché molte lingue scritte in tutto il mondo si possono rappresentare con meno di 256 caratteri. Dove poi un byte non basta (per rappresentare, per esempio, gli ideogrammi del cinese, del giapponese e del coreano), due byte, che permettono di rappresentare 216, ovvero 65.536, elementi diversi, di solito funzionano benissimo. Un byte è ideale anche per rappresentare le sfumature di grigio nelle fotografie in bianco e nero, perché l’occhio umano riesce a distinguere circa 256 tonalità di grigio. Per il colore sui display video, tre byte vanno bene per rappresentare le componenti di colore rossa, verde e blu.
La rivoluzione del personal computer è iniziata verso la fine degli anni Settanta e durante i primi anni Ottanta con i computer a 8 bit. Progressi tecnici successivi hanno raddoppiato il numero dei bit, da 16 a 32 a 64 (2 byte, 4 byte e 8 byte, rispettivamente). Per alcuni scopi speciali, esistono anche computer a 128 e a 256 bit.
La metà di un byte (cioè 4 bit) a volte viene chiamata nibble (a volte anche con l’ortografia nybble), ma non è una parola che si senta spesso quanto byte, nelle conversazioni.
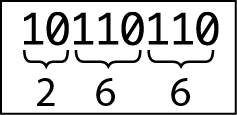
Poiché i byte si presentano spesso nel funzionamento interno dei computer, è comodo potersi riferire ai loro valori in modo più conciso che con una stringa di cifre binarie. Si può certamente usare l’ottale a questo scopo: nel caso del byte 10110110, per esempio, si possono dividere i bit in gruppi di tre a partire da destra, per poi convertire ciascun gruppo in ottale usando la tabella precedente, come nel caso della figura qui sotto.
Una rappresentazione di un numero binario in ottale.
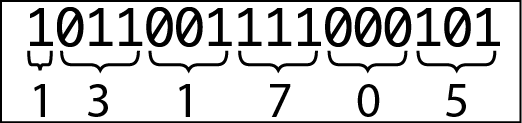
Il numero ottale 266 è più conciso di 10110110, ma c’è un’incompatibilità di fondo fra byte e sistema ottale: otto non è un multiplo di tre, il che significa che la rappresentazione ottale di un numero a 16 bit come quello nella prossima figura 12.2 non è la stessa della rappresentazione ottale dei due bit che compongono il numero a 16 bit nella figura successiva.
Rappresentazione ottale di un numero binario a 16 bit.
Rappresentazione ottale di due byte.
Perché le rappresentazioni di valori a più byte siano coerenti con le rappresentazioni dei singoli byte, ci serve un sistema di numerazione in cui ogni byte venga sempre diviso in un ugual numero di bit.
Potremmo dividere ciascun byte in quattro valori di 2 bit ciascuno: arriveremmo a un sistema in base quattro, o quaternario, ma probabilmente non è così conciso come avremmo voluto.
Altrimenti potremmo dividere il byte in due valori di 4 bit ciascuno, il che comporterebbe l’uso del sistema di numerazione in base 16.
Leggi anche: 5 risposte su… come imparare il coding in modo facile per principianti
Base 16. Ecco un sistema che non abbiamo ancora considerato, e per un buon motivo. Il sistema di numerazione in base 16 è chiamato codice esadecimale, e già la parola è un po’ un pasticcio. La maggior parte delle parole che iniziano con il prefisso esa (come esagono, esapodo o esametro) indicano sei di qualcosa. Qui invece esadecimale si riferisce a sedici. In inglese si dice hexadecimal e molti lo abbreviano in hex.
Il nome non è l’unica peculiarità del sistema di numerazione. In decimale, possiamo contare:
0 1 2 3 4 5 6 7 8 9 10 11 12…
In ottale, non ci servono più le cifre 8 e 9:
0 1 2 3 4 5 6 7 10 11 12…
Il codice esadecimale però è diverso, perché ha bisogno di più cifre del decimale. Se si conta in esadecimale succede qualcosa di questo genere:
0 1 2 3 4 5 6 7 8 9 qui ci serve qualche altro simbolo… 10 11 12
dove 10 (pronunciato uno-zero) è in effetti 16 in decimale. Che cosa possiamo usare per quei sei simboli mancanti? Dove li andiamo a pescare? Non ci sono arrivati dalla tradizione come il resto dei nostri simboli per i numeri, perciò la cosa più sensata sarebbe crearne sei nuovi, per esempio quelli della prossima figura.
Sei simboli per il codice esadecimale.
A differenza dei simboli usati per la maggior parte dei nostri numeri, questi hanno il vantaggio di potersi ricordare facilmente e di identificarsi con le quantità effettive che rappresentano. C’è un cappello da cowboy da 10 galloni, un pallone da football americano (11 giocatori per squadra), una dozzina di ciambelle, un gatto nero (associato al numero sfortunato 13), una luna piena che si forma 14 giorni dopo la luna nuova, e un pugnale che ci ricorda l’assassinio di Giulio Cesare alle idi (15) di marzo.
Ma no. Sfortunatamente (o forse con grande sollievo), non useremo palloni e ciambelle per scrivere i numeri esadecimali. Sarebbe possibile, ma non è così. La notazione esadecimale di uso comune invece garantisce che tutti vadano in confusione e ci rimangano. Le sei cifre esadecimali mancanti sono rappresentate dalle prime sei lettere dell’alfabeto, cosicché possiamo contare:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12…
La prossima tabella 12.2 mostra le conversioni fra sistemi binario, esadecimale e decimale.
Conversione fra i sistemi binario, esadecimale e decimale.
| Binario | Esadecimale | Decimale |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | A | 10 |
| 1011 | B | 11 |
| 1100 | C | 12 |
| 1101 | D | 13 |
| 1110 | E | 14 |
| 1111 | F | 15 |
Non è piacevole usare le lettere per rappresentare numeri (e la confusione aumenta quando si usano numeri per rappresentare lettere), ma il codice esadecimale è qui e ci resterà. Lo si usa per un motivo solamente: per rappresentare i valori dei byte nel modo più conciso possibile, e lo fa molto bene.
Un byte è composto da 8 bit, ovvero due cifre esadecimali comprese fra 00 e FF. Il byte 10110110 corrisponde al numero esadecimale B6, il byte 01010111 è il numero esadecimale 57.
Ora, B6 è ovviamente in esadecimale per la presenza della lettera, ma 57 potrebbe essere un numero decimale. Per evitare ulteriore confusione, ci serve un modo per distinguere facilmente numeri decimali ed esadecimali. Il modo esiste: in effetti, esistono circa 20 modi diversi di denotare i numeri esadecimali in diversi linguaggi e ambienti di programmazione. In questo articolo userò una h minuscola dopo il numero, per esempio B6h o 57h.
La tabella che segue elenca alcuni numeri esadecimali corrispondenti a 1 byte e i loro equivalenti decimali.
Rappresentazioni equivalenti nei sistemi binario, esadecimale e decimale.
| Binario | Esadecimale | Decimale |
|---|---|---|
| 00000000 | 00h | 0 |
| 00010000 | 10h | 16 |
| 00011000 | 18h | 24 |
| 00100000 | 20h | 32 |
| 01000000 | 40h | 64 |
| 01100100 | 64h | 100 |
| 10000000 | 80h | 128 |
| 11000000 | C0h | 192 |
| 11001000 | C8h | 200 |
| 11100000 | E0h | 224 |
| 11110000 | F0h | 240 |
| 11111111 | FFh | 255 |
Come quelli binari, anche i numeri esadecimali spesso vengono scritti con gli zero iniziali, per rendere chiaro che si lavora con un numero specifico di cifre. Per numeri binari più lunghi, quattro cifre binarie corrispondono a una cifra esadecimale. Un valore a 16 bit, cioè 2 byte, è rappresentato da 4 cifre esadecimali. Un valore a 32 bit, cioè 4 byte, è rappresentato da 8 cifre esadecimali.
L’uso del codice esadecimale si è diffuso, ed è diventato comune scrivere lunghi numeri binari con trattini o spazi ogni quattro cifre. Per esempio, il numero binario 0010010001101000101011001110 spaventa un po’ meno se scritto nella forma 0010 0100 0110 1000 1010 1100 1110 o 0010-0100-0110-1000-1010-1100-1110, e la corrispondenza con le cifre esadecimali diventa più chiara.
Un numero binario suddiviso in gruppi di quattro bit e le cifre esadecimali corrispondenti. Questo è il numero esadecimale 2468ACE, che contiene tutte le cifre esadecimali pari in ordine crescente.
Chi abbia fatto qualcosa con HTML, l’Hypertext Markup Language usato per le pagine web in Internet, probabilmente conoscerà un uso comune dell’esadecimale. Ogni punto (pixel) colorato sullo schermo del computer è una combinazione di tre colori primari additivi: rosso, verde e blu (per questo si parla di colore RGB, da red, green, blue). L’intensità di ciascuna di queste tre componenti è data da un valore byte, il che significa che sono necessari tre byte per specificare un particolare colore. Spesso, sulle pagine HTML, il colore di un oggetto è indicato con un valore esadecimale a sei cifre, preceduto da un segno di diesis (o cancelletto). Per esempio, una sfumatura di rosso ha il valore di colore #E74536, il che significa un valore di E7h per il rosso, un valore 45h per il verde, e un valore 36h per il blu. Questo colore, in alternativa, può essere specificato, nelle pagine HTML, con i valori decimali equivalenti, per esempio in questo modo: rgb (231, 69, 54).
Sapendo che sono necessari tre byte per specificare il colore di ciascun pixel sullo schermo del computer, si può fare qualche calcolo e ricavarne qualche altra informazione: se lo schermo del nostro computer contiene 1920 pixel in orizzontale e 1080 pixel in verticale (le dimensioni standard per la televisione in alta definizione), il numero totale dei byte necessari per memorizzare un’immagine per quel monitor è 1920 moltiplicato 1080 moltiplicato 3 byte, ovvero 6.220.800 byte.
Ciascun colore primario può avere un valore compreso fra 0 e 256, il che significa che il numero totale delle combinazioni possibili è 256 per 256 per 256, ovvero 16.7777.216. In codice esadecimale quel numero è 100h per 100h per 100h, ovvero 1000000h.
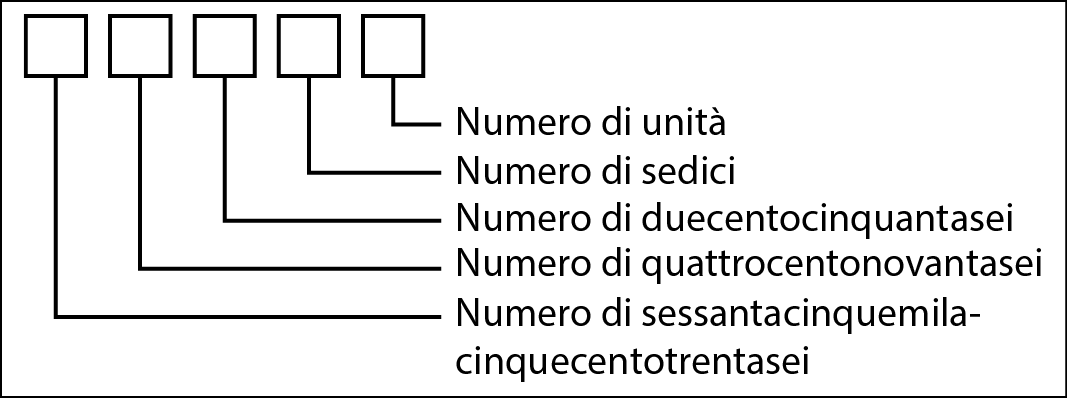
In un numero esadecimale, la posizione di ciascuna cifra corrisponde a una diversa potenza di 16, come si vede di seguito.
I valori posizionali per un numero in codice esadecimale.
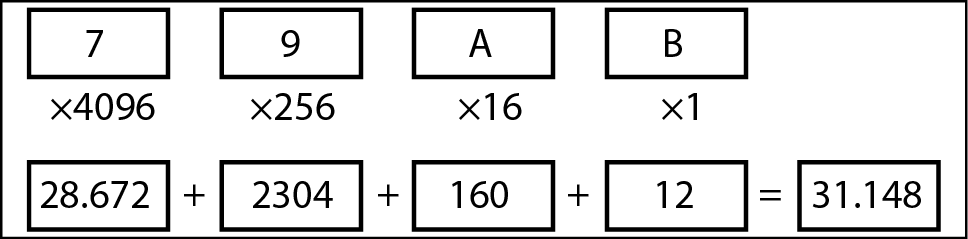
Il numero esadecimale 9A48Ch è:
Lo si può scrivere utilizzando le potenze di 16:
Oppure si possono usare gli equivalenti decimali di quelle potenze:
Si noti che non c’è ambiguità nello scrivere le singole cifre del numero (9, A, 4, 8, C) senza indicare la base. Un 9 da solo è un 9, non importa se in decimale o in esadecimale. E una A è ovviamente una cifra esadecimale, equivalente a 10 in decimale.
Convertire tutte le cifre in decimale ci permette di effettuare il calcolo:
La risposta è 631.948. Questo è il modo in cui si convertono i numeri esadecimali in decimale.
Nella figura sottostante è riportato un modello per convertire qualsiasi numero esadecimale a quattro cifre in decimale.
Uno schema per convertire un numero esadecimale in decimale.
Per esempio, vediamo la conversione di 79ACh. Ricordiamo che le cifre esadecimali A e C sono 10 e 12 in decimale, rispettivamente.
La conversione di numeri decimali in codice esadecimale in genere comporta delle divisioni. Se il numero è minore o uguale a 255, sapete che può essere rappresentato da 1 byte, ovvero due cifre esadecimali. Per calcolare quelle due cifre, dividiamo il numero per 16 e otterremo un quoziente e un resto. Per esempio, prendiamo il numero 182 decimale. Diviso per 16 dà 11 (che è B in esadecimale) con un resto di 6. L’equivalente esadecimale è B6h.
Conversione del numero 79ACh.
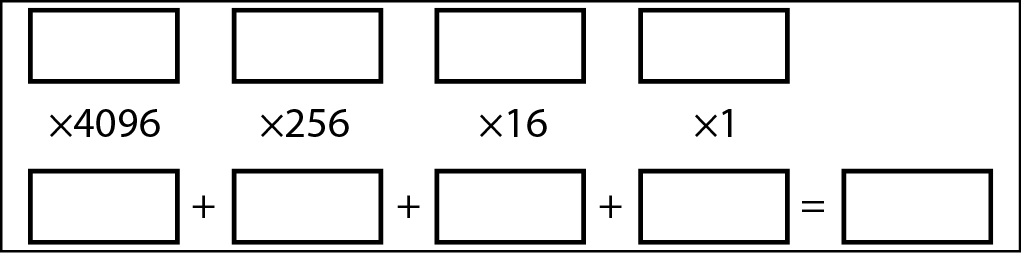
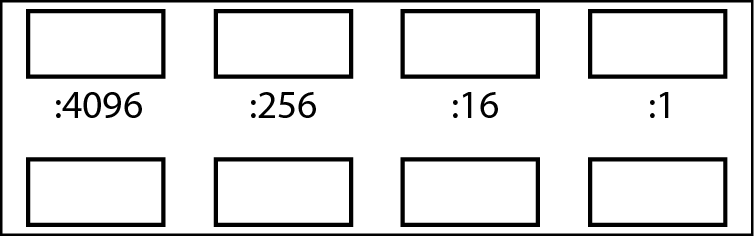
Se il numero decimale che vogliamo convertire è minore di 65.536, l’equivalente esadecimale avrà al massimo quattro cifre. La figura successiva mostra un modello per convertire in esadecimale un numero di questo tipo.
Uno schema per la conversione in esadecimale di numeri decimali minori di 65.536.
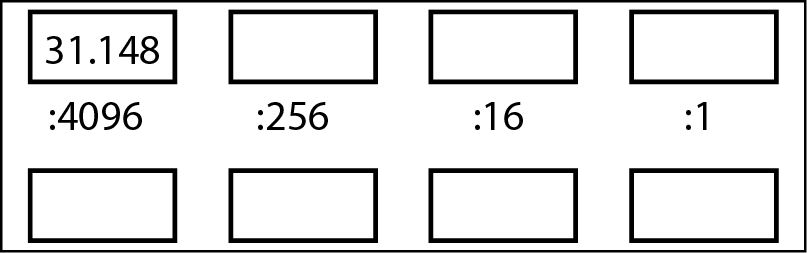
Si inizia inserendo tutto il numero decimale nella casella nell’angolo superiore sinistro (si veda la figura seguente).
Il primo passo nella conversione.
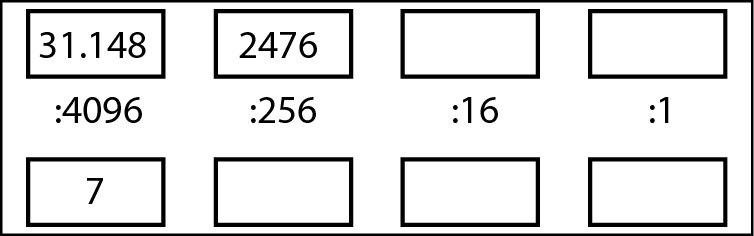
Dividiamo quel numero per 4096, ma solo per ottenere un quoziente e un resto. Il quoziente va nella prima casella in basso e il resto va nella casella successiva in alto (nella figura di seguito).
Il secondo passo nella conversione.
Ora dividiamo quel resto per 256, ma solo per ottenere un quoziente (9) e un nuovo resto (172). Continuiamo il procedimento fino alla fine (come si vede nella prossima figura).
Il risultato finale.
I numeri decimali 10 e 12 corrispondono alle cifre esadecimali A e C, perciò il risultato è 79ACh.
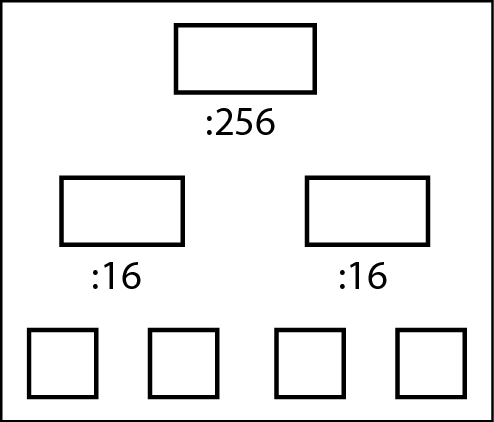
Un altro metodo per convertire i numeri decimali fino a 65.535 in codice esadecimale comporta separare prima il numero in due byte dividendolo per 256. Poi dividiamo per 16 ciascun byte. La figura seguente mostra un modello per farlo.
Un altro schema per la conversione di numeri decimali in codice esadecimale.
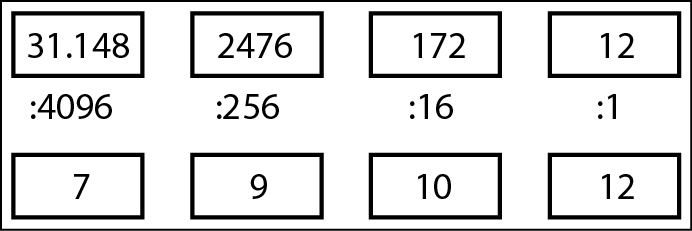
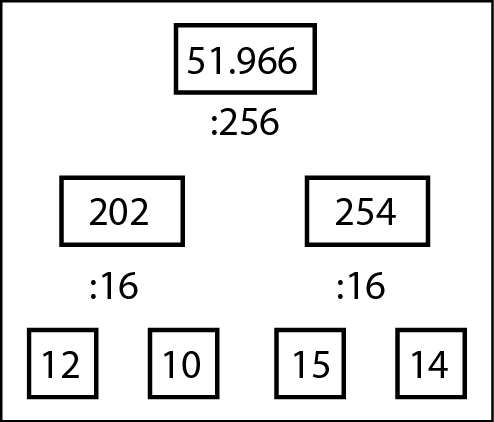
Iniziamo dalla casella più in alto. A ogni divisione, il quoziente va nella casella sottostante a sinistra, il resto in quella a destra. Per esempio, nella figura seguente si vede la conversione di 51.966.
La conversione in esadecimale di un numero decimale.
Le cifre esadecimali sono quelle corrispondenti ai numeri 12, 10, 15 e 14, ovvero CAFE: il risultato sembra una parola più che un numero.
Si possono usare la tabella e le normali regole del riporto per sommare numeri esadecimali. Per esempio:
La tabellina per l’addizione in esadecimale.
Come per ogni altra base numerica, all’esadecimale è associata una tabella dell’addizione (nella tabella di seguito).
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
| C | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B |
| D | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
| E | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D |
| F | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E |
Chi preferisse non eseguire questi calcoli a mano, sappia che le app Calcolatrice di Windows e macOS hanno una modalità programmatore che permette di effettuare calcoli in binario, ottale ed esadecimale e di effettuare conversioni dall’uno all’altro di questi sistemi di numerazione.
Questo articolo richiama contenuti dal capitolo 12 di Code.
Immagine di apertura di Karthik Garikapati su Unsplash.