“Vorrei un paio di jeans – taglia 32-28”, dissi. “Li vuole aderenti, comodi, taglia morbida, ampi, o molto ampi?”, rispose la commessa. “Li preferisce stone-washed, acid-washed, o invecchiati? Con zip o con bottoni? Scoloriti o normali?” Rimasi sbigottito. Qualche secondo più tardi balbettai qualcosa come: “Vorrei semplicemente dei jeans”.
– Barry Schwartz per favorire la trovabilità dell’informazione è utile fornire all’utente una molteplicità di stimoli. È pur vero, tuttavia, che un eccesso di opzioni può generare l’effetto opposto, cioè una sorta di imbarazzo della scelta congiunto a un effetto di spaesamento.
Questo è il senso del motto less is more, originariamente adottato dall’architetto Mies van der Rohe e poi propagatosi in molte discipline, dal design fino all’interazione uomo-macchina e uomo-informazione.
Fatte salve poche eccezioni, infatti, i gingilli tecnologici sono un terreno particolarmente favorevole alla proliferazione ingiustificata delle funzioni. E questo non solo ci fa perdere tempo, non è solo irritante, ma conduce a un vero e proprio disagio (e talvolta perfino a patologie come l’ansia, il panico, la depressione).
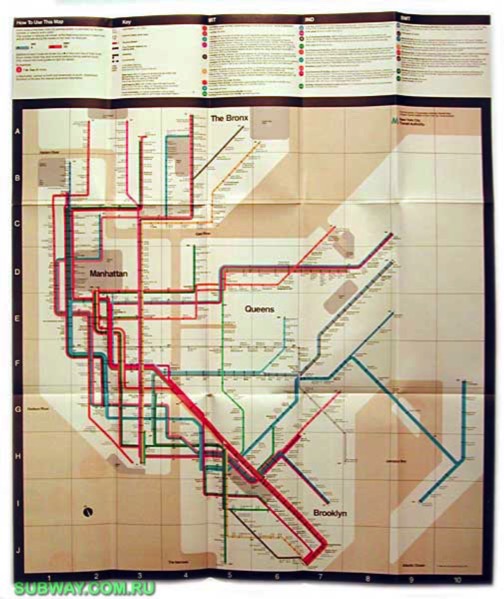
La mappa per la metropolitana di New York disegnata da Massimo Vignelli nel 1972 predilige la semplicità e la leggibilità rispetto all’esattezza della scala, usando solo linee a 90 e 45 gradi. Una magnifica dimostrazione che spesso “meno è più”. Fonte: http://subway.com.ru.
Scelta e stress
Lo stress da eccesso di scelta ha a che fare anzitutto con il nostro fuoco dell’attenzione, la cui peculiarità è di essere unico: ne esiste soltanto uno e non c’è modo di attivare un secondo fuoco dell’attenzione. O, che è lo stesso, non c’è modo di prestare attenzione (volontariamente o involontariamente che sia) a più di un oggetto nello stesso tempo.
Studi alla mano, Schwartz adduce anche altri fattori psicologici capaci di spiegare lo stress da eccesso di scelta.
Coda lunga e paradosso della scelta
I mercati attuali, anche grazie alle nuove tecnologie, si stanno evolvendo sempre più verso il cosiddetto modello della coda lunga: una forte differenziazione e personalizzazione dell’offerta, la tendenza a soddisfare contemporaneamente numerosi mercati di nicchia, cercando di vendere pochi prodotti in tante nicchie differenti, piuttosto che molti prodotti in un unico settore (Anderson, 2007). Ma questo aumento dell’offerta può portare con sé anche un aumento di stress dovuto all’eccesso di offerta. Questo è il paradosso della scelta.
Tuttavia il modello della coda lunga e il concetto di paradosso della scelta non sono antitetici fra loro, come a prima vista potrebbe sembrare. Infatti, il problema del sovraccarico informativo non è (sol)tanto un problema di quantità dell’informazione, ma anche (e soprattutto) un problema di qualità, ovvero del modo in cui tale mole di informazioni e beni è organizzata, presentata e resa reperibile. Spesso, infatti, il disordine o l’inappropriatezza contestuale (di tutto e di più) con cui beni e servizi sono presentati costituiscono il vero problema.
Copertine dei libri di Schwartz, The Paradox of Choice, e Anderson, La coda lunga.
La legge di Hick
Come conciliare allora queste due esigenze apparentemente opposte: economia della coda lunga da un lato, eccesso di informazione e paradosso della scelta dall’altro? La legge di Hick, fornendoci un modello matematico per la comprensione del fenomeno del paradosso della scelta, ci suggerisce anche le possibili soluzioni.
La legge di Hick dice che se ci sono n alternative equiprobabili, il tempo che impieghiamo a sceglierne una è proporzionale (a meno di una costante additiva) al logaritmo in base 2 del numero di scelte più 1:
tempo = a + b log2 (n + 1)
I coefficienti a e b della legge dipendono da alcune condizioni al contorno, fra le quali il modo in cui le scelte vengono presentate e il grado di abitudine dell’utente: se le scelte sono presentate in modo confuso, sia a sia b tendono a crescere, mentre l’abitudine tende a far diminuire b (Raskin, 2003, pp. 108-110).
A ogni modo, l’aspetto che più ci interessa è che la relazione espressa dalla legge di Hick fra il tempo di scelta e il numero di scelte possibili è logaritmica (cioè non lineare).
Perciò, a parità di condizioni (costanti a e b), all’aumentare del numero di opzioni aumenta senz’altro anche il tempo di reazione (per comodità, nel nostro esempio, non abbiamo sommato il +1 al numero delle scelte: ai fini di una stima applicare la formula senza il +1 è ininfluente):
- con 2 opzioni, log2 2 = 1
- con 4 opzioni, log2 4 = 2
- con 8 opzioni, log2 8 = 3
Viceversa, a parità di numero di scelte, sono le condizioni al contorno a e b a influire sul tempo di reazione. Ecco perché l’applicazione della formula ai menu va fatta con cautela.
Infatti, nel caso di una lista di opzioni disordinata (priva cioè di un qualche criterio logico riconoscibile da parte dell’utente), è difficile operare quella scomposizione mentale in categorie che la legge di Hick presuppone (l’utente sarà costretto a scorrere tutte le voci una per una); il tempo di scelta diventa allora lineare e la formula perde di significato.
Viceversa, se una lista di opzioni è presentata secondo un criterio logico (per esempio alfabetico), risulta possibile utilizzare un criterio di scomposizione delle scelte (per esempio l’utente andrà alla lettera di interesse e solo a questo punto scorrerà tutte le voci fino a trovare quella cercata); il tempo in questo caso è in relazione non lineare con il numero di alternative e la legge è pertinente.
In quest’ultimo caso, la formula di Hick dice che scegliere una volta da un menu di 8 voci è più rapido che scegliere due volte da un menu di 4 voci ciascuno. Vale a dire che, a parità di numero di elementi, le strutture “larghe” (insieme di opzioni su uno stesso livello) sono preferibili alle strutture “profonde” (insieme di opzioni su più livelli). Infatti, nel primo caso la formula è:
a + b log2 8 = a + 3b
(poiché log2 8 = 3), e nel secondo è
2 (a + b log2 4) = 2a + 4b
(poiché log2 4 = 2); e dato che a < 2a e 3b < 4b risulta:
a + 3b < 2a + 4b
La legge di Hick ci fa capire che il tempo necessario per compiere una scelta non è soltanto funzione del numero di scelte possibili, ma anche del criterio in base al quale le scelte sono presentate. E, in certi casi, tale criterio diviene molto più importante del numero di scelte stesso.
Sulla scorta di queste considerazioni, vedremo ora quali strategie sia possibile adottare per fronteggiare il paradosso della scelta.
Organizzare, raggruppare
La bilancia elettronica fai-da-te in uso presso la gran parte dei supermercati ci offre un ottimo esempio di paradosso della scelta.
La pulsantiera delle bilance degli ipermercati soffre del paradosso della scelta.
Nella maggioranza dei casi, il display per selezionare il tipo di frutta o verdura contiene dai 30 ai 60 o più tasti, disposti in ordine numerico. A ciascun codice corrisponde un prodotto; il codice numerico associato al prodotto è riportato nei cartellini della merce esposta.
Quali sono gli inconvenienti posti da questa soluzione?
- Al momento del prelievo della merce dal banco, l’utente deve memorizzare il codice prodotto associato, andare subito alla bilancia, depositare la busta e digitare il codice; questo comporta uno sforzo mnemonico, e capita spesso che nel caso non si pesi subito la merce ci si dimentichi il codice nel frattempo. (Alcune coppie si organizzano in questo modo: uno va alla bilancia, l’altro detta il numero ad alta voce dal banco merci.)
- L’associazione codice-prodotto non rimane stabile nel tempo, ma è giocoforza sottoposta a variazioni più o meno frequenti in base al ricambio dei prodotti stessi. Perciò se anche l’utente abituale avesse con il tempo memorizzato i codici dei prodotti acquistati più frequentemente, questo sforzo verrebbe comunque vanificato.
In un ipermercato hanno trovato una soluzione per migliorare la “performance”. Anziché proporre tutte le tipologie di frutta e verdura assieme, la bilancia invita prima a selezionare una categoria tra:
- frutta
- verdura
- frutta secca
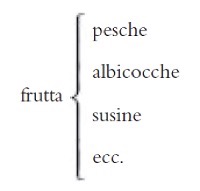
Solo dopo aver scelto una di queste tre voci vengono presentate le relative tipologie di prodotto. Per esempio:
Un esempio di bilancia che permette di ridurre il paradosso della scelta, facendo prima scegliere la categoria di prodotto (frutta, verdura, frutta secca), poi i prodotti della categoria selezionata.
Abbiamo detto che, in base alla legge di Hick, scegliere una volta da un menu di 8 voci richiede meno sforzo che scegliere due volte da un menu di 4 voci ciascuno. Allora, la soluzione di scomporre un menu di 30-60 voci in un menu principale (a un primo livello) e vari sottomenu (a un secondo livello) dovrebbe aumentare e non diminuire il carico cognitivo e il paradosso della scelta.
In realtà, i tasti della bilancia rappresentano uno scenario in cui la legge di Hick non è valida, perché la disposizione delle opzioni segue un ordine (quello numerico) che non offre alcun vantaggio all’utente. L’ordine numerico non corrisponde a un criterio significativo o utile dal punto di vista del compito che l’utente deve svolgere: ritrovare fra tutti i numeri quello relativo al prodotto scelto. Anche l’impiego di icone (fra l’altro non su tutti i tasti), in questo caso, serve a poco: l’elevato numero di opzioni vanifica il vantaggio delle icone, riducendone la riconoscibilità.
I tasti rappresentano quindi una lista di opzioni casuale o non significativa: proprio per questo essa non è soggetta alla legge di Hick. In contesti di questo tipo, al crescere del numero degli elementi, il tempo di scelta cresce in modo lineare (e non più logaritmico come vuole la formula di Hick), poiché (come abbiamo detto al paragrafo precedente) non è possibile per l’utente operare quella suddivisione mentale degli elementi della lista in categorie.
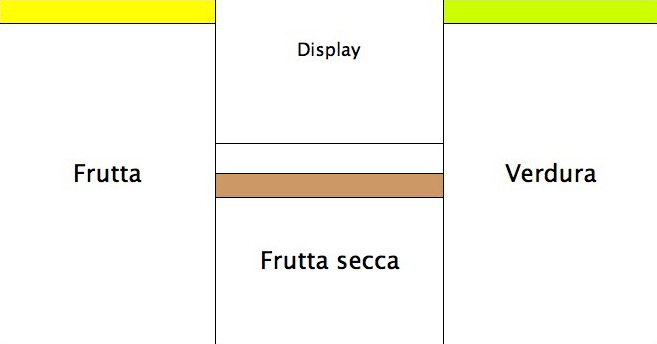
Una soluzione ancora migliore potrebbe essere quella indicata nella prossima figura: tutti i tasti vengono visualizzati insieme, ma raggruppati per settore (Frutta, Verdura, Frutta secca). In questo modo si ottiene una lista di opzioni su un unico livello, ma con un ordine logico; la legge di Hick in questo caso torna a essere pertinente e i tempi di scelta sono ancora più bassi rispetto alla soluzione precedente.
Un’ulteriore soluzione per ridurre il paradosso della scelta nelle bilance fai-da-te.
Due modi di organizzare/raggruppare
In conclusione, la strategia “organizzare/raggruppare” è una di quelle applicabili per ridurre il tempo di scelta e il relativo carico cognitivo in due direzioni:
- nell’elencare le voci di un menu, cercando di seguire un criterio significativo per l’utente (tale da aiutarlo a operare raggruppamenti mentali delle voci, secondo la legge di Hick);
- se non vi è modo di fornire un ordine significativo alle opzioni di un menu, allora può essere utile operando un raggruppamento su più livelli (in tal caso la scelta su più livelli sarà senz’altro preferibile a quella su uno, in quanto mancando un ordine logico la legge di Hick non si applica e la struttura larga non è più preferibile a quella profonda). In questo caso, introdurre dei raggruppamenti equivale a introdurre un criterio di ordinamento/classificazione e, quindi, a ridurre il tempo di reazione.
Bibliografia
- Anderson, Chris. 2007. La coda lunga: Da un mercato di massa a una massa di mercati. Torino: Codice Edizioni. Edizione originale col titolo The Long Tail: Why the Future of Business Is Selling Less of More (Hyperion, 2006)
- Raskin, Jef. 2003. Interfacce a misura d’uomo. Milano: Apogeo. Edizione originale col titolo The Human Interface: New Directions for Designing Interactive Systems (Addison-Wesley, 2000).
- Schwartz, Barry. 2004. The Paradox of Choice: Why More Is Less. New York: HarperCollins.
Questo articolo è basato su alcuni brani tratti dal capitolo 5 di Architettura dell’informazione.