Il gioco delle tre porte

Il paradosso di Monty Hall, dal nome del presentatore che lo popolarizzò, è un argomento di quelli che scuotono certezze consolidate e spingono a imparare qualcosa di nuovo.

Il gioco propone una sfida ai concorrenti. Devono indovinare quale delle tre porte nasconde un premio, con una piccola variante. Il concorrente deve innanzitutto scegliere la porta che ritiene “giusta”. Tuttavia il presentatore non apre tale porta per scoprire se nasconde il premio. Piuttosto, apre un’altra porta che non nasconde il premio. Poi chiede: “Mantieni la scelta o preferisci cambiarla con l’altra porta chiusa?”.

Considerate questo: se doveste aiutare il concorrente, gli direste di cambiare o di mantenere la scelta? Alternativamente, pensate che la cosa faccia differenza? Quasi tutti direbbero che la cosa non farebbe alcuna differenza. E quasi tutti sbaglierebbero.

In effetti, esattamente questo problema e la sua soluzione sono comparsi in un articolo di Marilyn vos Savant, ritenuta la persona più intelligente al mondo. La Savant diede la risposta corretta. È meglio cambiare, di fattore pari a 2 a 1.

Questa risposta, corretta, sembra incredibile alla maggior parte della popolazione. Qualcosa come 10.000 persone hanno scritto alla Savant, dicendole che si sbagliava. Circa 1000 di loro erano laureati. Ora le rendiamo ragione.

Ragioniamo con Bayes

Potete ricorrere alla statistica per ottenere la risposta corretta. Potete anche trovare del codice sul Web che applichi tecniche statistiche nell’eseguire 10.000 simulazioni e risolvere questa domanda. La risposta sarà quasi corretta. Una semplice Rete di Bayes impiega circa tre minuti a costruirsi e risolvere con esattezza questo problema.

Le probabilità che questo libro torni utile sono elevate.

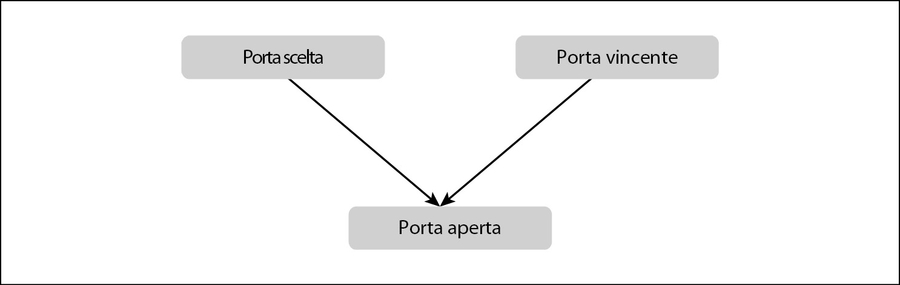
Come abbiamo detto è possibile realizzare una rete manualmente collegando le variabili. Qui costruiremo una piccola rete collegando tre eventi: la porta scelta, la porta aperta e la porta vincente.

La più semplice rappresentazione di una Rete di Bayes ha l’aspetto rappresentato nella prossima figura. Sappiamo che la porta vincente può essere ognuna delle tre e che la porta scelta può essere ognuna delle tre. Tuttavia, la porta aperta dal presentatore dipende sia dalla porta che avete scelto sia dalla porta vincente.

La rete per il problema delle tre porte.

Nella figura, una freccia va dalla porta scelta alla porta aperta. Un’altra freccia va dalla porta vincente alla porta aperta. La direzione di tali frecce conta, questa volta, perché la porta aperta dipende, o è condizionata, dalle altre due scelte.

Ognuno di questi tre elementi è chiamato nodo. Aumentiamo la nostra potenza esplorativa osservando ciò che si trova al loro interno. Ogni nodo contiene in pratica una tabella corrispondente a ciò che accade con le tre porte.

Innanzitutto configuriamo il nodo mostrando le probabilità che apriate ciascuna porta: un terzo per ciascuna porta. Poi configuriamo il nodo mostrando le probabilità che si tratti della porta vincente: anche qui un terzo per ciascuna porta. Otteniamo un risultato che è di una semplicità estrema, come possiamo vedere nella figura qui sotto.

Ora configuriamo l’ultimo e il più complesso dei nodi. Una volta che abbiamo creato i primi due nodi e li abbiamo connessi al terzo, nel software appare automaticamente la tabella che descrive questo nodo, pronta da compilare. Come abbiamo detto, nelle Reti di Bayes, è importante vedere ciò che si sta facendo.

I primi due nodi della rete.

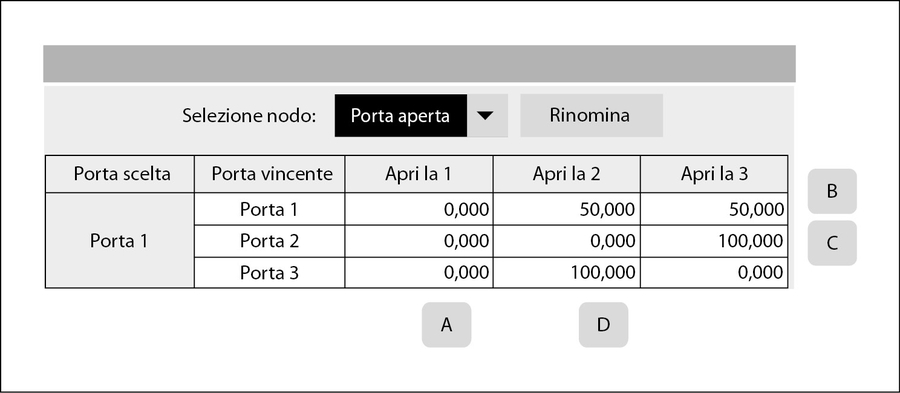
Poiché questa tabella è più complessa, la suddivideremo in parti, partendo dalla figura seguente. Questa presenta ciò che accade se avete scelto la Porta 1. Sopra la lettera A, vedete che la Porta 1 NON viene aperta se è quella prescelta, indipendentemente dalla porta che risulterà vincente. Questa è una regola di base del gioco.

Parte del terzo nodo – avendo scelto la Porta 1.

Se avete scelto la Porta 1 e questa è in effetti quella vincente, potete vedere (prima riga della tabella nell’ultima figura) che le probabilità di aprire la Porta 2 o la Porta 3 sono del 50 percento ciascuna. Tale riga è identificata dalla lettera B.

Finora tutto OK. Ora, se avete scelto la Porta 1 e la porta vincente è la 2, il presentatore deve scegliere se aprire la Porta 3 o rivelare il premio. Pertanto qui le probabilità legate alle altre porte non sono più le stesse – in pratica sono pari a 0 e al 100 percento, è una scelta obbligata. Potete vederlo sulla riga contrassegnata dalla lettera C.

Infine, la stessa condizione si verifica se avete scelto la Porta 1 e la vincente è la 3. Il presentatore deve aprire la Porta 2. La probabilità che lo farà è del 100 percento (lettera D).

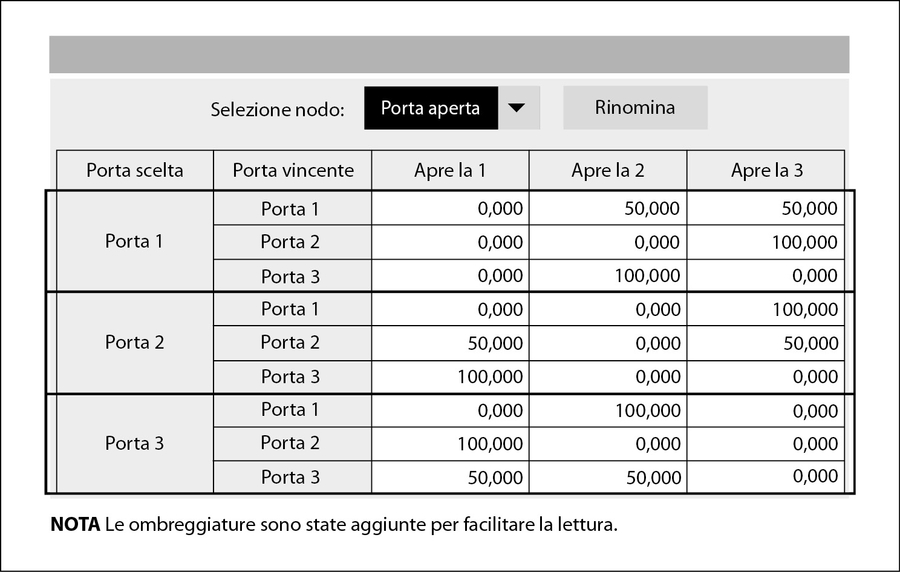
Una volta compilati i valori corretti per la Porta 1, diventa relativamente semplice compilare i valori corretti per le Porte 2 e 3. L’intera tabella del terzo nodo è illustrata nella figura sottostante. Abbiamo aggiunto delle ombreggiature per separare le sezioni della tabella corrispondenti a ciascuna delle porte che potreste aver scelto. Per il resto ci siamo limitati a riportare i numeri. Di nuovo, la rete ha creato la tabella da sola, una volta connessi fra loro i tre nodi.

Il terzo nodo.

E ora la risposta, sorprendente

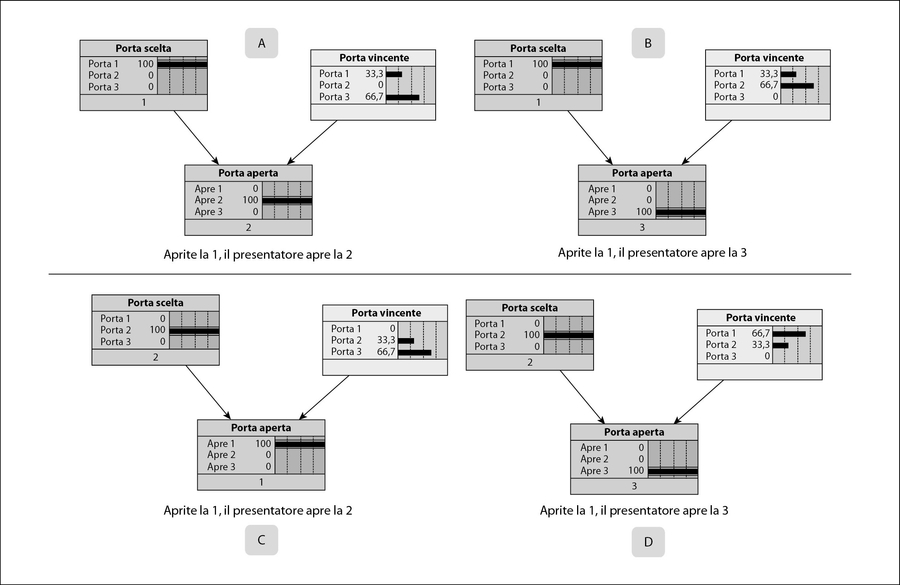
Forse questo è un buon momento per fare un bel respiro. Come potete vedere nella figura successiva, dovreste cambiare porta.

Abbiamo incluso quattro possibili risultati, ammettendo di aver scelto la Porta 1 o la Porta 2. Questi risultati dovrebbero condurre tutti i lettori (o quasi) che sarebbe esattamente la stessa cosa iniziando dalla Porta 3.

Abbiamo ripetuto l’esecuzione della rete con due clic. Il primo sulla porta scelta, che è salita al 100 percento. Poi sulla porta aperta dal presentatore, che è salita anch’essa al 100 percento.

Quanto è probabile che il premio sia dietro ciascuna porta.

Alla lettera A, vediamo ciò che accade se si parte scegliendo la Porta 1 e il presentatore apre la Porta 2. Le probabilità compaiono automaticamente nel nodo della porta vincente. Le probabilità che il premio si trovi dietro la vostra porta sono del 33,3 percento. Per l’altra porta, la Porta 3, le probabilità sono del 66,7 percento.

Alla lettera B, vediamo ciò che accade se si parte scegliendo la Porta 1 e il presentatore apre la Porta 3. Le probabilità per la Porta 2 sono del 66,7 percento e quelle per la vostra porta sono del 33,3 percento.

Per confermare che la cosa non riguarda esclusivamente la Porta 1, mostriamo ciò che accadrebbe iniziando dalla Porta 2. Alla lettera C, vedete il risultato se il presentatore risponde aprendo la Porta 1. Le probabilità per l’altra porta sono ancora del 66,7 percento. Infine, se il presentatore apre la Porta 3, le probabilità per la porta che non avete scelto sono ancora pari al 66,7 percento.

Di nuovo, questo sottolinea una proprietà importante delle reti. Se modificate una variabile, cambia anche ogni variabile a essa connessa. Vediamo che porta aperta ha una freccia in arrivo da porta vincente. Ciononostante quando modifichiamo porta aperta, cambia anche la variabile che a essa conduce.

Questo articolo richiama contenuti da AI Marketing.