Risposte a cavallo tra codice, elettronica di base e microprocessori
- Perché a un codice possono bastare due bit
- Perché il numero 65.536, nei computer, è una cifra tonda
- A chi dobbiamo i computer e il loro codice
- Quali sono o sono stati i primi linguaggi di programmazione importanti
- Come funziona il codice Morse
Perché a un codice possono bastare due bit
Ascoltate, figli miei, e sentirete / della cavalcata di Paul Revere nella notte.
Lo scrisse Henry Wadsworth Longfellow; forse non è stato particolarmente accurato nel descrivere come Paul Revere avvertì le colonie americane dell’arrivo dei soldati inglesi, ma ci ha fornito comunque un esempio su cui riflettere dell’uso dei bit per comunicare informazioni importanti:
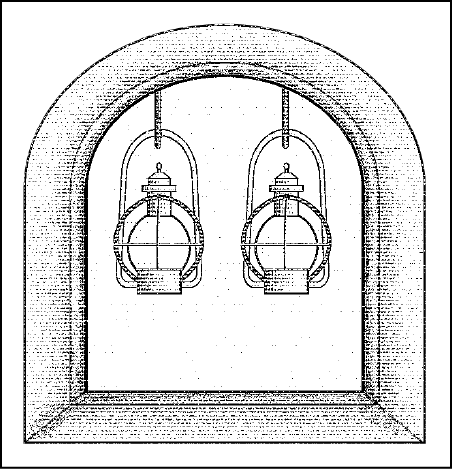
Disse all’amico: “Se gli inglesi marciano / per terra o per mare dalla città stanotte, / Esponi una lanterna in alto sul campanile / della torre di North Church come un segnale / Una se via terra e due se via mare…”
Per riassumere, l’amico di Paul Revere aveva due lanterne. Se gli inglesi fossero arrivati via terra, avrebbe dovuto mettere una sola lanterna accesa sul campanile della chiesa. Se fossero arrivati via mare, avrebbe dovuto esporre entrambe le lanterne accese.
Longfellow non cita esplicitamente tutte le possibilità: passa sotto silenzio una terza possibilità, cioè che gli inglesi non stiano ancora arrivando. Dà per scontato che questa circostanza venga comunicata dall’assenza di lanterne accese sul campanile della chiesa.
Supponiamo che le due lanterne siano effettivamente due oggetti stabilmente presenti sul campanile. Normalmente non sono accese e questo significa che gli inglesi non stanno ancora arrivando.
Due lanterne spente: tutto è tranquillo.
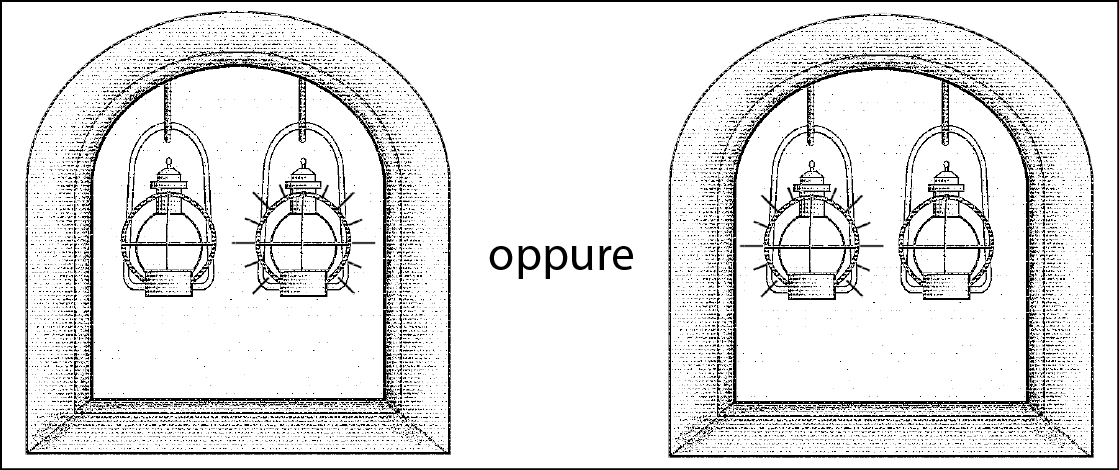
Se una lanterna è accesa, significa che gli inglesi stanno arrivando via terra.
Una lanterna accesa: gli inglesi arrivano via terra.
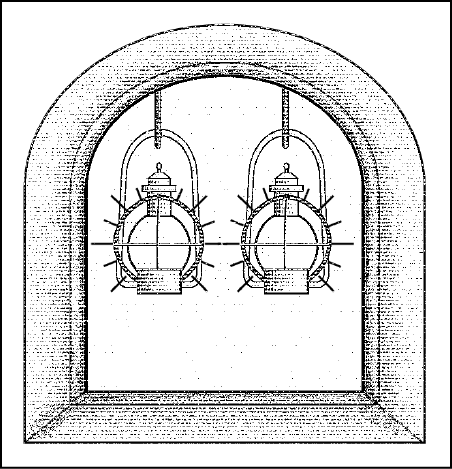
Se sono accese entrambe le lanterne, vuol dire che gli inglesi stanno arrivando via mare.
Due lanterne accese: gli inglesi arrivano via mare.
Ciascuna lanterna è un bit e può essere rappresentata da uno 0 o da un 1. La storia del nastro giallo dimostra che è necessario un solo bit per indicare una possibilità su due. Se Paul Revere avesse avuto bisogno di essere avvertito solamente dell’arrivo degli inglesi e non anche della direzione di provenienza, sarebbe stata sufficiente una lanterna: accesa in caso di attacco, spenta altrimenti.
Per veicolare una possibilità su tre è necessaria un’altra lanterna. Se c’è quella seconda lanterna, però, i due bit consentono di comunicare il verificarsi di una su quattro possibilità.
- 00 = Gli inglesi non attaccheranno stanotte.
- 01 = Stanno arrivando da terra.
- 10 = Stanno arrivando da terra.
- 11 = Stanno arrivando dal mare.
Quello che fece Paul Revere fermandosi a tre possibilità era in effetti abbastanza sofisticato. Nel gergo della teoria delle comunicazioni, ha usato la ridondanza per annullare l’effetto del rumore. Nella teoria delle comunicazioni si usa la parola rumore per indicare qualsiasi cosa interferisca con la comunicazione. Una cattiva connessione del cellulare è un esempio ovvio di rumore che interferisce con una comunicazione telefonica. Una telefonata di solito va a buon fine anche in presenza di rumore, perché il linguaggio parlato è fortemente ridondante. Non abbiamo bisogno di sentire ogni sillaba di ogni parola per capire che cosa viene detto.
Nel caso delle lanterne sul campanile, il rumore poteva avere a che fare con l’oscurità della notte e con la distanza a cui si trovava Paul Revere rispetto al campanile, due fattori che avrebbero potuto impedirgli di distinguere una lanterna dall’altra. Ecco il passaggio cruciale nel poema di Longfellow.
Ed ecco! Mentre guarda, in alto sul campanile, / Uno scintillio, poi un bagliore di luce! / Salta in sella, gira le briglie, / Ma si ferma un po’ e osserva, finché bene in vista / Sul campanile brilla una seconda luce!
Certamente non sembra che Paul Revere fosse nelle condizioni di capire esattamente quale delle due lanterne fosse stata accesa per prima.
L’idea essenziale qui è che l’informazione rappresenta una scelta fra due o più possibilità. Quando parliamo con un’altra persona, ogni parola che pronunciamo è una scelta fra tutte le parole del dizionario. Se numerassimo tutte le parole del dizionario da 1 a 351.482, potremmo condurre una conversazione accurata utilizzando i numeri anziché le parole. (Ovviamente entrambi i partecipanti dovrebbero avere dizionari uguali in cui le parole siano numerate nello stesso modo, e anche una buona dose di pazienza.)
L’altra faccia della medaglia è che qualsiasi informazione possa essere ridotta alla scelta fra due o più possibilità può essere espressa mediante bit. Va da sé che esistono moltissime forme di comunicazione umana che non rappresentano scelte fra possibilità discrete e che sono vitali per la nostra esistenza. Questo è il motivo per cui le persone non intrattengono relazioni romantiche con i computer (o almeno speriamo non lo facciano). Se qualcosa non può essere espresso in parole, immagini o suoni, non riusciremo a codificarlo in bit. Né vorremo farlo.
Perché il numero 65.536, nei computer, è una cifra tonda
si dice di una RAM che memorizzi 65.536 byte che ha la capacità di 64 kilobyte, o 64 K, o 64 KB, il che a prima vista può lasciare un po’ perplessi. Per quale pazza aritmetica 65.536 diventa 64 kilobyte?
Il valore 210 è 1.024, che è il valore comunemente noto come kilobyte. Il prefisso kilo o chilo (dal greco khilioi, che significa mille) viene usato spesso nel sistema metrico: un chilogrammo è pari a 1.000 gramnni, un chilometro equivale a 1.000 metri. Qui però sto dicendo che un kilobyte è pari a 1.024 byte, non 1.000 byte.
Leggi anche: Robot: costruirli e programmarli in 5 risposte
Il problema è che il sistema metrico si basa sulle potenze di 10, mentre i numeri binari sono basati sulle potenze di 2 e i due sistemi non si incontreranno mai. Le potenze di 10 sono 10, 100, 1.000, 10.000, 100.000 e così via; le potenze di 2 sono 2, 4, 8, 16, 32, 64 e così via. Non esiste potenza intera di 10 che sia uguale a qualche potenza intera di 2.
Ogni tanto, però, ce ne sono alcune abbastanza vicine. Sì, 1.000 è piuttosto vicino a 1.024, o, per dirlo in termini matematicamente più corretti mediante un segno approssimativamente uguale a:
210 ≅ 103
Non vi è nulla di magico in questa relazione. Tutto quello che implica è che una particolare potenza di 2 è approssimativamente uguale a una particolare potenza di 10. Questa piccola scappatoia consente di parlare comodamente di un kilobyte di memoria quando in realtà si vuol parlare di 1.024 byte. Per far capire che sapete bene di che cosa parliamo, dobbiamo dire 64 K o 64 kilobyte o sessantacinquemilacinquecentotrentasei byte.
Ogni ulteriore bit di indirizzo raddoppia la quantità di memoria indirizzabile. Ogni riga della prossima tabella corrisponde a un raddoppio.
I kilobyte e i loro equivalenti in byte.
| Numero di kilobyte | Numero di byte equivalente | Byte equivalenti come potenza | |
|---|---|---|---|
| 1 kilobyte | 1024 byte | 210 byte | ≅ 103 byte |
| 2 kilobyte | 2048 byte | 211 byte | |
| 4 kilobyte | 4096 byte | 212 byte | |
| 8 kilobyte | 8192 byte | 213 byte | |
| 16 kilobyte | 16.384 byte | 214 byte | |
| 32 kilobyte | 32.768 byte | 215 byte | |
| 64 kilobyte | 65.536 byte | 216 byte | |
| 128 kilobyte | 131.072 byte | 217 byte | |
| 256 kilobyte | 262.144 byte | 218 byte | |
| 512 kilobyte | 524.288 byte | 219 byte | |
| 1.024 kilobyte | 1.048.576 byte | 220 byte | ≅ 106 byte |
Si noti che anche i numeri di kilobyte nella prima colonna sono potenze di 2.
Con la stessa logica che ci permette di dire che 1024 byte sono un kilobyte, possiamo dire che 1024 kilobyte sono un megabyte. (La parola greca megas significa grande.) Megabyte si abbrevia in MB. Così continua il progressivo raddoppio di memoria (nella tabella seguente).
La parola greca gigas significava gigante, così 1.024 megabyte prendono il nome di gigabyte, abbreviato in GB.
Analogamente, un terabyte (teras significa mostro) è uguale a 240 byte (all’incirca 1012), ovvero 1.099.511.627.776 byte. Terabyte si abbrevia TB.
Un kilobyte è pari a circa mille byte, un megabyte è circa un milione di byte, un gigabyte è circa un miliardo di byte e un terabyte è circa un bilione (mille miliardi) di byte.
I megabyte e i loro equivalenti in byte.
| Numero di megabyte | Numero di byte equivalente | Byte equivalenti come potenza | |
|---|---|---|---|
| 1 megabyte | 1.048.576 byte | 220 byte | ≅ 106 byte |
| 2 megabyte | 2.097.152 byte | 221 byte | |
| 4 megabyte | 4.194.304 byte | 222 byte | |
| 8 megabyte | 8.388.608 byte | 223 byte | |
| 16 megabyte | 16.777.216 byte | 224 byte | |
| 32 megabyte | 33.554.432 byte | 225 byte | |
| 64 megabyte | 67.108.864 byte | 226 byte | |
| 128 megabyte | 134.217.728 byte | 227 byte | |
| 256 megabyte | 268.435.456 byte | 228 byte | |
| 512 megabyte | 536.870.912 byte | 229 byte | |
| 1.024 megabyte | 1.073.741.824 byte | 230 byte | ≅ 109 byte |
Per salire ad altezze che pochi hanno mai raggiunto, un petabyte è pari a 250 byte, ovvero 1.125.899.906.842.624 byte, che è approssimativamente 1015, ovvero un biliardo (un milione di miliardi). Un exabyte è pari a 260 byte, ovvero 1.152.921.504.606.846.976 byte, approssimativamente 1018, ovvero un trilione (un miliardo di miliardi).
Tanto per dare qualche termine di confronto, i computer desktop che si potevano acquistare nel 1999 avevano normalmente 32 o 64 MB, qualche volta 128 MB di memoria ad accesso casuale. Nel momento in cui scrivo questa seconda edizione, nel 2021, i computer desktop hanno in genere 4, 8 o 16 GB di RAM. (Non facciamo confusione: non ho detto ancora nulla di memoria permanente, che si conserva quando si spegne la corrente, sotto forma di dischi rigidi e unità a stato solido. Qui sto parlando solo di RAM.)
Spesso, ovviamente, si abbreviano le cose quando si parla. Qualcuno che ha 65.536 byte di memoria dirà: Ho 64 K (e ho viaggiato nel tempo dall’anno 1980). Qualcuno che ha 33.554.432 byte dirà: Ho 32 mega. Chi ha 8.589.934.592 byte di memoria dirà: Ho 8 giga.
Qualcuno parlerà di kilobit o megabit (notate: bit e non byte), ma succede raramente se si parla di memoria. Quasi sempre, a proposito di memoria, si parla di numero di byte, non di bit. Di solito quando in una conversazione compaiono i kilobit o i megabit, si sta parlando di dati trasmessi su un cavo o via etere, in genere a proposito delle connessioni internet ad alta velocità a banda larga e in genere all’interno di espressioni come kilobit al secondo o megabit al secondo.
A chi dobbiamo i computer e il loro codice
Nel novembre del 1937, un ricercatore dei Bell Labs, George Stibitz (1904-1995) prese un paio di relè usati nei circuiti di commutazione telefonica. Sul tavolo della cucina, combinò quei relè con batterie, due lampadine e due interruttori fatti con strisce di metallo tagliate da lattine di alluminio. Era un addizionatore a 1 bit, che Stibitz poi chiamò Model K, perché era stato costruito sul tavolo della cucina (kitchen, in inglese).
L’addizionatore Model K era quello che in seguito sarebbe stato definito una proof of concept, che dimostrava come i relè potessero eseguire operazioni aritmetiche. I Bell Labs autorizzarono un progetto per sviluppare ulteriormente l’idea e nel 1940 era operativo il Complex Number Computer. Era formato da oltre 400 relè ed era dedicato alla moltiplicazione di numeri complessi, numeri costituiti da una parte reale e una parte immaginaria. (I numeri immaginari sono radici quadrate di numeri negativi e sono utili in applicazioni scientifiche e tecniche.) La moltiplicazione di due numeri complessi richiede quattro moltiplicazioni distinte e due addizioni. Il Complex Number Computer era in grado di trattare numeri complessi con parti reali e immaginarie fino a otto cifre decimali. Per eseguire una di quelle moltiplicazioni impiegava circa un minuto.
Quello non è stato il primo computer basato su relè. Cronologicamente il primo fu costruito da Conrad Zuse (1910-1995), uno studente di ingegneria che nel 1935 iniziò a costruire una macchina nell’appartamento dei genitori a Berlino. La sua prima macchina, chiamata Z1, non usava relè ma ne simulava il funzionamento in forma puramente meccanica. La sua macchina Z2 usava relè e poteva essere programmata mediante fori perforati in una vecchia pellicola cinematografica da 35 mm.
Intanto, intorno al 1937, uno studente laureato di Harvard, Howard Aiken (1900-1973) aveva bisogno di eseguire una grande quantità di calcoli ripetitivi e questo condusse a una collaborazione fra l’Università di Harvard e IBM, che alla fine produsse l’Automated Sequence Controlled Calculator (ASCC), poi chiamato Harvard Mark I, completato nel 1943. Quando era in funzione, il ticchettio dei relè produceva un suono molto particolare, che a detta di qualcuno era come se ci fosse una stanza piena di signore che sferruzzavano a maglia. Il Mark II è stato la più grande fra le macchine basate su relè: ne conteneva 13 mila. Lo Harvard Computation Laboratory, diretto da Aiken, ha tenuto i primi corsi di computer science.
Questi computer basati sui relè (chiamati anche computer elettromeccanici perché combinava elettricità e dispositivi meccanici) sono stati i primi computer digitali funzionanti.
La parola digitali per descrivere questi computer fu coniata da George Stibitz nel 1942 per distinguerli dai calcolatori analogici, che allora erano di uso comune già da qualche decennio.
Uno dei grandi computer analogici era l’Analizzatore Differenziale costruito da un docente del MIT, Vannevar Bush (1890-1974) e dai suoi studenti fra il 1927 e il 1932. Quella macchina usava dischi rotanti, perni e ingranaggi per risolvere equazioni differenziali, che sono equazioni particolari nel campo dell’analisi mtematica. La soluzione di un’equazione differenziale non è un numero ma una funzione e l’Analizzatore Differenziale stampava un grafico di quella funzione su carta.
Le origini dei computer analogici possono essere fatte risalire alla Macchina per la previsione delle maree progettata dal fisico William Thomson (1824-1907), poi Lord Kelvin. Negli anni Sessanta dell’Ottocento, Thomson immaginò un modo per analizzare l’andamento delle maree e per suddividerlo in una serie di curve sinusoidali diverse per frequenza e ampiezza. Nelle parole di Thomson, l’obiettivo della sua Macchina per la previsione delle maree era sostituire ottone al cervello nella grande operazione meccanica di calcolare i costituenti elementari di tutto l’innalzamento e l’abbassamento delle maree. In altre parole, usava ruote, ingranaggi e pulegge per sommare le curve sinusoidali componenti e stampare il risultato su un rotolo di carta, mostrando l’andamento futuro delle maree.
Sia l’Analizzatore Differenziale, sia la Macchina per la previsione delle maree erano in grado di stampare grafici, ma la cosa interessante è che lo facevano senza calcolare i numeri che definivano il grafico. Questa è una caratteristica dei computer analogici.
Già nel 1879 William Thomson conosceva la differenza fra computer analogici e digitali, anche se usava una terminologia diversa. Chiamava macchine calcolatrici continue gli strumenti come quello per la previsione delle maree, per distinguerli dalle macchine puramente aritmetiche, come le idee grandiose, ma solo parzialmente realizzate, di macchine calcolatrici di Babbage.
Thomson si riferiva ai famosi lavori del matematico inglese Charles Babbage (1791-1871). A posteriori, si potrebbe dire che Babbage abbia rappresentato un’anomalia storica, perché tentò di costruire un computer digitale molto prima che fossero comuni quelli analogici.
Quali sono o sono stati i primi linguaggi di programmazione importanti
Il più vecchio dei linguaggi di alto livello ancora in uso oggi (anche se ampiamente rivisto nel corso degli anni) è il FORTRAN. Molti fra i primi linguaggi hanno nomi scritti in lettere maiuscole perché sono acronimi. FORTRAN è una combinazione delle prime tre lettere della parola FORmula e delle prime quattro della parola TRANslation. Sviluppato alla IBM intorno alla metà degli anni Cinquanta per i computer della serie 704, per molti anni è stato considerato il linguaggio d’elezione per scienziati e tecnici. Ha un supporto molto ampio per i numeri in virgola mobile e addirittura anche per quelli complessi, che sono combinazioni di numeri reali e immaginari.
COBOL (che sta per COmmon Business Oriented Language) è un altro dei primi linguaggi di programmazione ancora in uso, soprattutto negli istituti finanziari. fu creato da un comitato di rappresentanti di industrie americane e del Dipartimento della Difesa degli Stati Uniti nel 1959, ma fu influenzato dai primi compilatori di Grace Hopper. In parte fu progettato in modo che i manager, che probabilmente non avrebbero scritto effettivamente i programmi, potessero almeno leggere il codice di programma e verificare se faceva quello che avrebbe dovuto fare. (Nella vita reale, però, succede di rado.)
Un linguaggio di programmazione che ha avuto un’influenza profonda ma non è più usato oggi (se non forse da qualche hobbista) è ALGOL. Il nome deriva da ALGOrithmic Language, ma è anche il nome della seconda stella per luminosità nella costellazione di Perseo. Progettato da un comitato internazionale nel 1957 e 1958, è il precursore diretto di molti linguaggi di uso generale che hanno avuto grande diffusione nell’ultimo mezzo secolo. È stato il primo ad applicare un’idea che poi ha preso il nome di programmazione strutturata. Ancora oggi c’è chi parla di linguaggi di programmazione ALGOL-like.
Anche se versioni di FORTRAN, COBOL e ALGOL erano disponibili per i computer domestici, nessuno di questi linguaggi ha avuto un impatto sul mondo delle macchine di piccole dimensioni come quello che ha avuto il BASIC.
BASIC (Beginner’s All-purpose Symbolic Instruction Code) fu sviluppato nel 1964 da John Kemeny e Thomas Kurtz della facoltà di matematica a Dartmouth per un sistema a divisione di tempo. La maggior parte degli studenti di Dartmouth non erano laureandi in matematica o ingegneria e perciò non si poteva pretendere che affrontassero la complessità dei computer e una sintassi di programmazione difficile. Uno studente a un terminale invece poteva creare un programma in BASIC semplicemente scrivendo enunciati BASIC preceduti da numeri. I numeri indicavano l’ordine degli enunciati del programma. Il primo programma BASIC nel primo manuale d’istruzione mai pubblicato per quel linguaggio era il seguente.
10 LET X = (7 + 8) / 3
20 PRINT X
30 END
Il linguaggio di programmazione Pascal ereditò gran parte della sua struttura dall’ALGOL, ma mutuò qualche caratteristica anche dal COBOL. Progettato verso la fine degli anni Sessanta da Niklaus Wirth (nato nel 1934), professore svizzero di informatica, ebbe molta fortuna fra i primi programmatori dell’IBM PC, ma in una forma molto specifica, cioè come Turbo Pascal, introdotto dalla Borland International nel 1983 al modico prezzo di 49,95 dollari. Scritto da uno studente danese, Anders Hejlsberg (nato nel 1960), il Turbo Pascal era fornito con un IDE (Integrated Development Environment, ambiente di sviluppo integrato): text editor e compilatore erano riuniti in un unico programma, che rendeva facile programmare rapidamente. Gli ambienti di sviluppo integrati erano diffusi sui grandi mainframe, ma il Turbo Pascal ne segnò l’arrivo anche su macchine più piccole.
Pascal ebbe un’influenza importante su Ada, un linguaggio sviluppato per il Dipartimento della Difesa degli Stati Uniti. Il nome è un omaggio ad Augusta Ada Byron, promotrice della Macchina analitica di Charles Babbage.
Poi c’è il C, un linguaggio di programmazione molto utilizzato, creato fra il 1969 e il 1973 ai Bell Telephone Laboratories, in gran parte da Dennis M. Ritchie. Spesso le persone si chiedono perché sia stato chiamato C. La risposta è semplice: derivava da un linguaggio precedente chiamato B, che era una versione semplificata del BCPL (Basic CPL), a sua volta derivato dal CPL (Combined Programming Language).
La maggior parte dei linguaggi di programmazione cerca di eliminare ogni traccia del linguaggio assembly, come gli indirizzi di memoria; il C invece no, mette a disposizione uno strumento particolare, il puntatore, che è fondamentalmente un indirizzo di memoria. I puntatori erano molto comodi per i programmatori che sapevano come usarli, ma pericolosi per tutti (o quasi) gli altri. In conseguenza della possibilità di scrivere in aree importanti della memoria, i puntatori erano una fonte comune di errori. Allen I. Holub, un programmatore, scrisse un libro sul C che si intitolava Enough Rope to Shoot Yourself in the Foot (ovvero Abbastanza corda da spararsi nel piede).
C è stato il nonno di una serie di linguaggi meno pericolosi, che in più hanno introdotto la possibilità di lavorare con oggetti, entità di programmazione che combinano codice e dati in una forma molto strutturata. I più famosi fra questi linguaggi sono C++, creato nel 1985 dall’informatico danese Bjarne Stroustrup (nato nel 1950); Java, progettato da James Gosling (nato nel 1955) alla Oracle Corporation nel 1995; e C#, progettato inizialmente da Anders Hejlsberg alla Microsoft nel 2000. Nel momento in cui scrivo, uno dei più utilizzati è un altro linguaggio che ha subito l’influenza del C, cioè Python, progettato nel 1991 dal programmatore olandese Guido von Rossum (nato nel 1956).
Come funziona il codice Morse
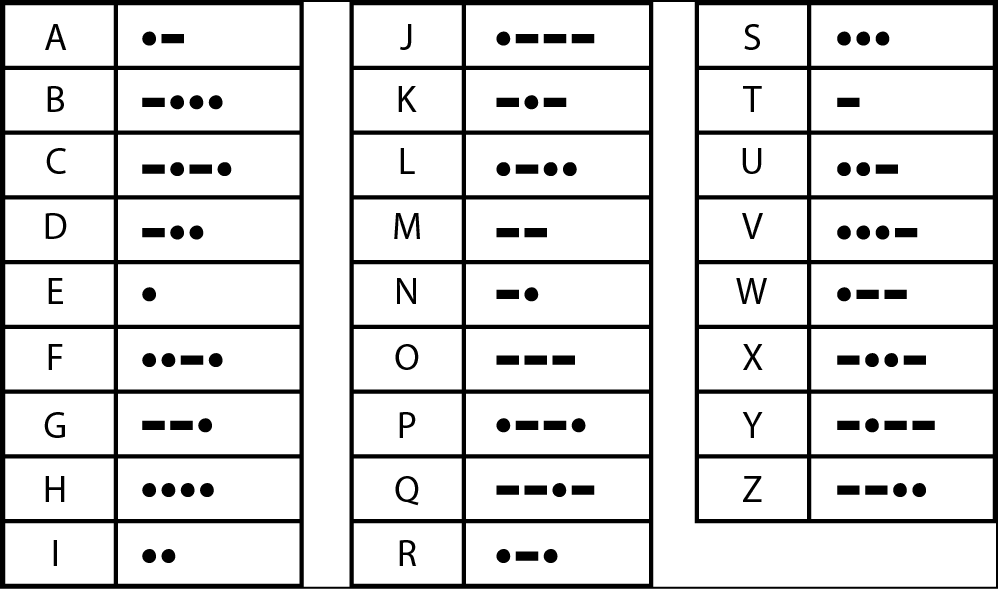
Il codice Morse fu inventato intorno al 1837 da Samuel Finley Breese Morse (1791-1872). Fu poi sviluppato ulteriormente da altri, in particolare da Alfred Vail (1807-1859), e si è evoluto in un paio di versioni diverse. Il sistema descritto qui è conosciuto più formalmente come codice Morse internazionale.
L’invenzione del codice Morse va a braccetto con l’invenzione del telegrafo. Come il codice Morse costituisce una buona introduzione alla natura dei codici, il telegrafo contiene hardware il cui funzionamento è simile a quello di un computer.
Ricevere codice Morse e ritradurlo in parole è notevolmente più difficile e richiede più tempo che non inviarlo, perché bisogna procedere a ritroso e individuare la lettera che corrisponde a una particolare sequenza codificata di punti e linee. Se non abbiamo memorizzato i codici e riceviamo un linea-punto-linea-linea, dobbiamo scorrere la tabella lettera per lettera finché non scopriamo, finalmente, che si tratta della lettera Y.
Il codice Morse.
Il problema è che abbiamo una tabella che ci dà la traduzione:
lettera dell’alfabeto → codice Morse a punti e linee
ma non abbiamo una tabella che proceda in senso inverso:
codice Morse a punti e linee → lettera dell’alfabeto
Quando si inizia a usare il codice Morse, una tabella del genere farebbe comodo, ma non è affatto ovvio come costruirla. Per punti e linee l’ordine alfabetico non ha senso.
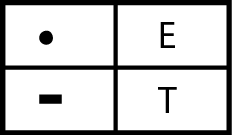
Dimentichiamoci allora dell’ordine alfabetico. Forse un metodo migliore sarebbe organizzare i codici in gruppi in base al numero di punti e linee che contengono. Per esempio, una sequenza che contenga solo un punto o una linea può rappresentare solo due lettere, che sono E e T.
Lettere rappresentate da un solo punto o una sola linea nel codice Morse.
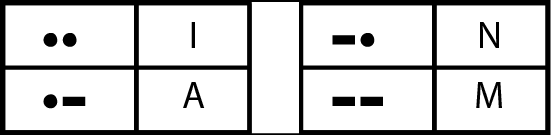
Una combinazione di esattamente due punti o linee ci mette a disposizione quattro altre lettere: I, A, N, M.
Lettere rappresentate con due simboli del codice Morse.
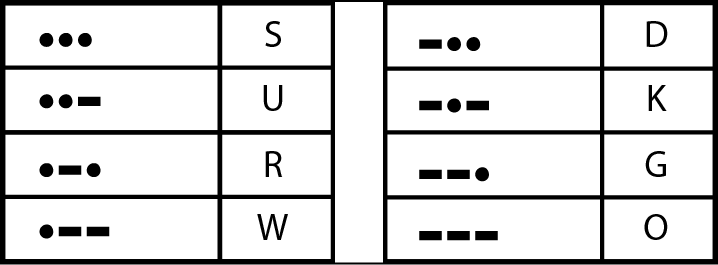
Una configurazione di tre punti o linee ci dà altre otto lettere.
Le lettere rappresentate da tre simboli del codice Morse.
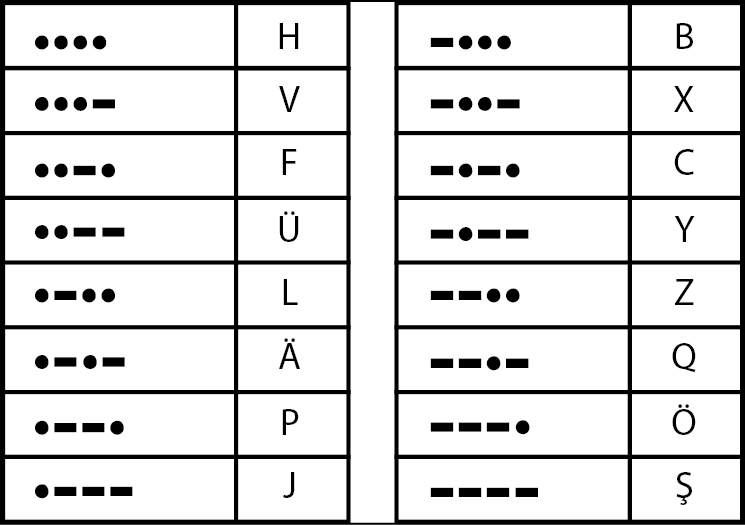
Infine (se vogliamo fermarci prima di affrontare i numeri e i segni di interpunzione), le sequenze di quattro punti o linee ci danno altri 16 caratteri.
Lettere rappresentate con quattro simboli del codice Morse.
Nell’insieme, queste quattro tabelle contengono 2 + 4 + 8 + 16 = 30 lettere, 4 più delle 26 necessarie per l’alfabeto inglese. Per questo, noteremo che quattro codici nell’ultima tabella sono per lettere accentate: tre con Umlaut e una con cediglia.
Possiamo riassumere tutto questo in una semplice tabella.
Numero di codici ottenibili con un dato numero di punti o linee.
| Numero di punti o linee | Numero di codici |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
Ciascuna delle quattro tabelle ha il doppio di codici della precedente, perciò la prima ha 2 codici, la seconda 2 × 2 codici, la terza ha 2 × 2 × 2 codici. Ecco una rappresentazione in forma di tabella di questo fatto.
Il numero di codici espresso come prodotto.
| Numero di punti e linee | Numero di codici |
|---|---|
| 1 | 2 |
| 2 | 2 × 2 |
| 3 | 2 × 2 × 2 |
| 4 | 2 × 2 × 2 × 2 |
Quando abbiamo a che fare con un numero moltiplicato per se stesso, possiamo iniziare a usare gli esponenti per indicare le potenze. Per esempio, 2 × 2 × 2 × 2 può essere scritto nella forma 24 (2 alla quarta potenza). I numeri 2, 4, 8, 16 sono tutti potenze di 2 perché li si può calcolare moltiplicando 2 per se stesso. Possiamo riassumere anche questo fatto nella semplice tabella che segue.
Il numero di codici espresso come potenza di 2.
| Numero di punti e linee | Numero di codici |
|---|---|
| 1 | 21 |
| 2 | 2 |
| 3 | 23 |
| 4 | 24 |
Questa tabella è diventata molto semplice. Il numero dei codici è semplicemente 2 elevato alla potenza uguale al numero di punti e linee:
numero di codici = 2numero di punti e linee
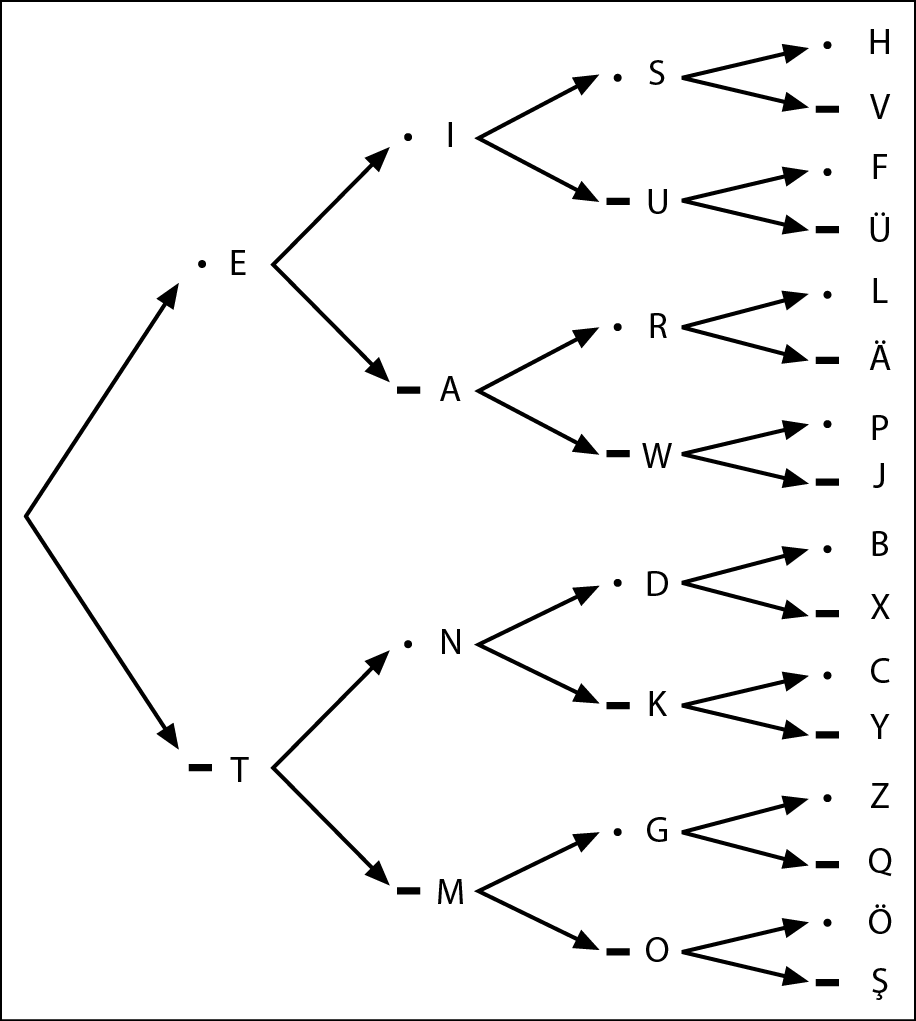
Per rendere ancora più facile il processo di decodifica del codice Morse, si potrebbe disegnare qualcosa di simile al diagramma ad albero della figura qui sotto.
Diagramma ad albero per la decodifica del codice Morse.
Questo diagramma mostra le lettere che corrispondono a ciascuna particolare sequenza di punti e linee consecutivi. Per decodificare una particolare sequenza, seguiamo le frecce da sinistra verso destra. Per esempio, supponiamo di voler sapere quale lettera corrisponde al codice punto-linea-punto. Iniziamo da sinistra e scegliete il punto; poi continuiamo verso destra seguendo le frecce e scegliamo prima la linea e poi un altro punto. La lettera è la R, mostrata accanto al terzo punto.
Se ci si riflette, probabilmente la costruzione di un diagramma di questo genere è stata necessaria proprio per definire inizialmente il codice Morse. Innanzitutto, garantisce che non si commetta l’errore stupido di usare lo stesso codice per due lettere diverse; in secondo luogo, si ha la certezza di usare tutti i codici possibili senza rendere lunghe più del necessario le sequenze di punti e linee.
Questo articolo richiama contenuti da Code.
Immagine di apertura di Jake Walker su Unsplash.