5 risposte per capire meglio come funzionano e come si programmano gli algoritmi
- Che cos’è la notazione Big O
- Perché gli algoritmi migliori eseguono poche operazioni
- Perché alcuni algoritmi non hanno (ancora) una soluzione certa
- Perché gli algoritmi ricorsivi fanno girare la testa
- Come funzionano gli alberi binari dentro gli algoritmi
Che cos’è la notazione Big O
Big O è una speciale notazione che dice quanto è veloce un algoritmo. Ci capiterà spesso di utilizzare algoritmi scritti da altri, ed è bene sapere se sono veloci o lenti.
I tempi di esecuzione di un algoritmo crescono a velocità differenti
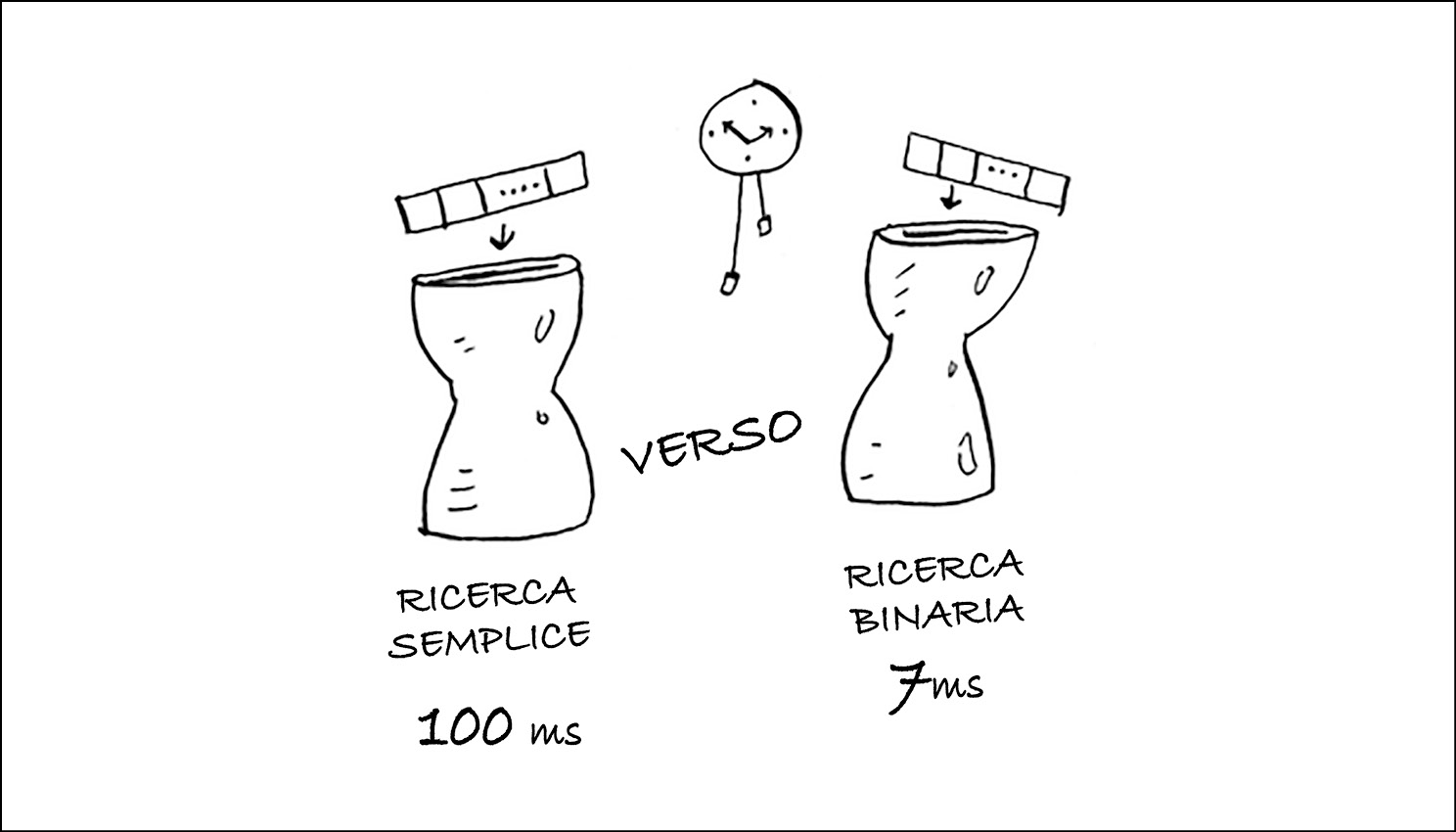
Bob sta scrivendo un algoritmo di ricerca per la NASA. Il suo algoritmo verrà utilizzato quando la navicella sta per atterrare sulla Luna e aiuterà a calcolare il punto di atterraggio.
Questo è un esempio di come il tempo di esecuzione di due algoritmi può crescere a velocità differenti. Bob sta cercando di decidere tra una ricerca semplice e una ricerca binaria. L’algoritmo deve essere veloce e corretto. Da un lato, la ricerca binaria è più veloce, e Bob ha solo 10 secondi per calcolare il punto di atterraggio, altrimenti la navicella andrà fuori rotta. D’altra parte, la ricerca semplice è più facile da scrivere, e ci sono meno possibilità che contenga bug. E Bob non vuole davvero lasciare ai bug il compito di far atterrare la navicella! Per maggiore sicurezza, Bob decide di cronometrare entrambi gli algoritmi con una lista di 100 elementi.
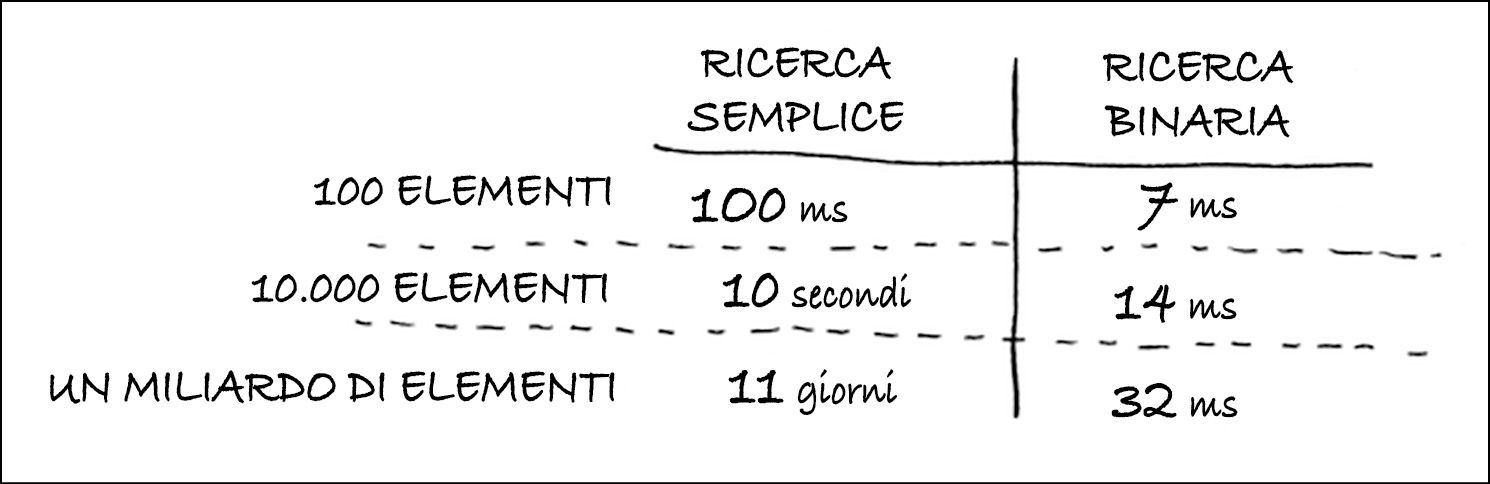
Supponiamo che ci voglia 1 millisecondo (ms) per controllare un elemento. Con una ricerca semplice, Bob deve controllare 100 elementi, quindi la ricerca impiega 100 millisecondi. Al contrario, con la ricerca binaria deve controllare solo 7 elementi (log2 100 vale circa 7), e così la ricerca richiede solo 7 millisecondo. Ma realisticamente, la lista conterrà più di un miliardo di elementi. In tal caso, quanto tempo impiegherà la ricerca semplice? E quanto tempo impiegherà la ricerca binaria? Assicuriamoci di avere in mente una risposta a queste due domande, prima di continuare a leggere.
Tempo di esecuzione per la ricerca semplice e per la ricerca binaria, con una lista di 100 elementi.
Bob esegue la ricerca binaria con un miliardo di elementi, e impiega 30 millisecondi (log2 1.000.000.000 è circa 30). 30 ms!, pensa. La ricerca binaria è circa quindici volte più veloce della ricerca semplice, perché la ricerca semplice ha richiesto 100 ms con 100 elementi e la ricerca binaria ha impiegato 7 ms. Quindi una ricerca semplice su un miliardo di elementi richiederà 30 × 15 = 450 ms, giusto? Molto al di sotto della mia soglia di 10 secondi. Bob decide di adottare una ricerca semplice. È la scelta giusta?
No. Bob ha torto. Torto marcio. Il tempo di esecuzione per una ricerca semplice con un miliardo di elementi sarà di un miliardo di millisecondi, ovvero 11 giorni! Il problema è che i tempi di esecuzione per la ricerca binaria e per la ricerca semplice non crescono alla stessa velocità.
I tempi di esecuzione crescono a velocità molto differenti.
All’aumentare del numero di elementi, la ricerca binaria richiede solo un po’ più di tempo per essere eseguita, mentre la ricerca semplice richiede molto più tempo. Quindi, man mano che la lista dei numeri diventa più grande, la ricerca binaria diventa sempre più veloce della ricerca semplice. Bob pensava che la ricerca binaria fosse sempre 15 volte più veloce della ricerca semplice, ma non è così. Se la lista contiene un miliardo di elementi, sarà circa 33 milioni di volte più veloce. Ecco perché non è sufficiente conoscere il tempo di esecuzione di un algoritmo: è necessario sapere come aumenta il tempo di esecuzione all’aumentare delle dimensioni della lista. È qui che entra in gioco la notazione Big O.
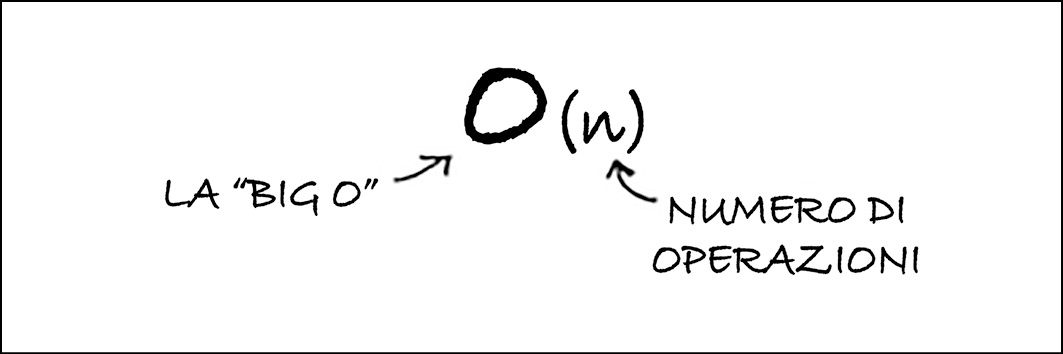
La notazione Big O dice quanto è veloce un algoritmo. Per esempio, supponiamo di avere una lista di dimensioni n. La ricerca semplice deve controllare ogni elemento, quindi ci vorranno n operazioni. Il tempo di esecuzione nella notazione Big O è O(n). E… dove sono i secondi? Non ce ne sono: Big O non dà una velocità in secondi. La notazione Big O consente di confrontare il numero di operazioni. Dice quanto velocemente cresce l’algoritmo.
Ecco un altro esempio. La ricerca binaria richiede operazioni log n per controllare una lista di dimensioni n. Qual è il tempo di esecuzione nella notazione Big O? È O(log n). In generale, la notazione Big O è scritta come segue.
L’aspetto della notazione Big O.
Questo dice il numero di operazioni che eseguirà un algoritmo. Si chiama notazione Big O ed è rappresentata da una “O” maiuscola.
Perché gli algoritmi migliori eseguono poche operazioni
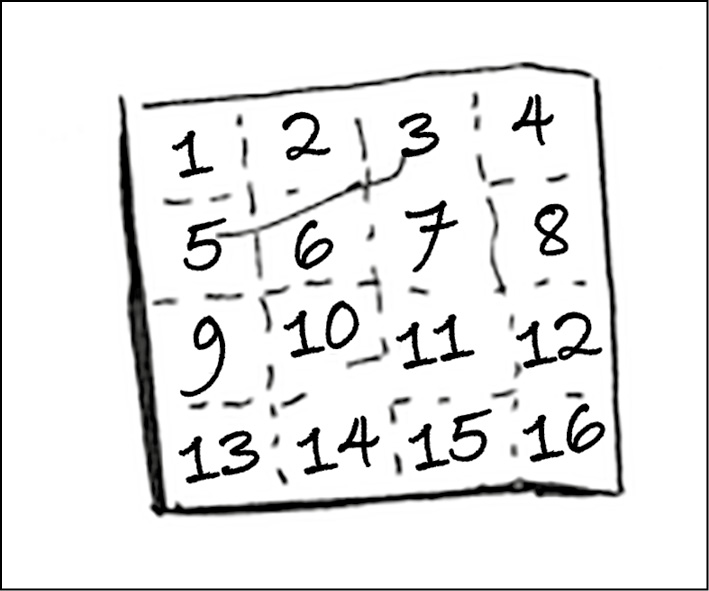
Ecco un esempio pratico che possiamo seguire a casa con dei fogli di carta e una matita. Supponiamo di dover disegnare una griglia di 16 caselle.
Qual è un buon algoritmo per disegnare questa griglia?
Algoritmo 1
Un modo per farlo è disegnare 16 caselle, una alla volta. Ricordiamo: la notazione Big O conta il numero di operazioni. In questo esempio, un’operazione è disegnare una casella. Dobbiamo disegnare 16 caselle. Quante operazioni ci vorranno, disegnando una casella per volta?
Disegnare la griglia una casella alla volta.
Occorrono 16 passi per disegnare 16 caselle. Qual è il tempo di esecuzione di questo algoritmo?
Algoritmo 2
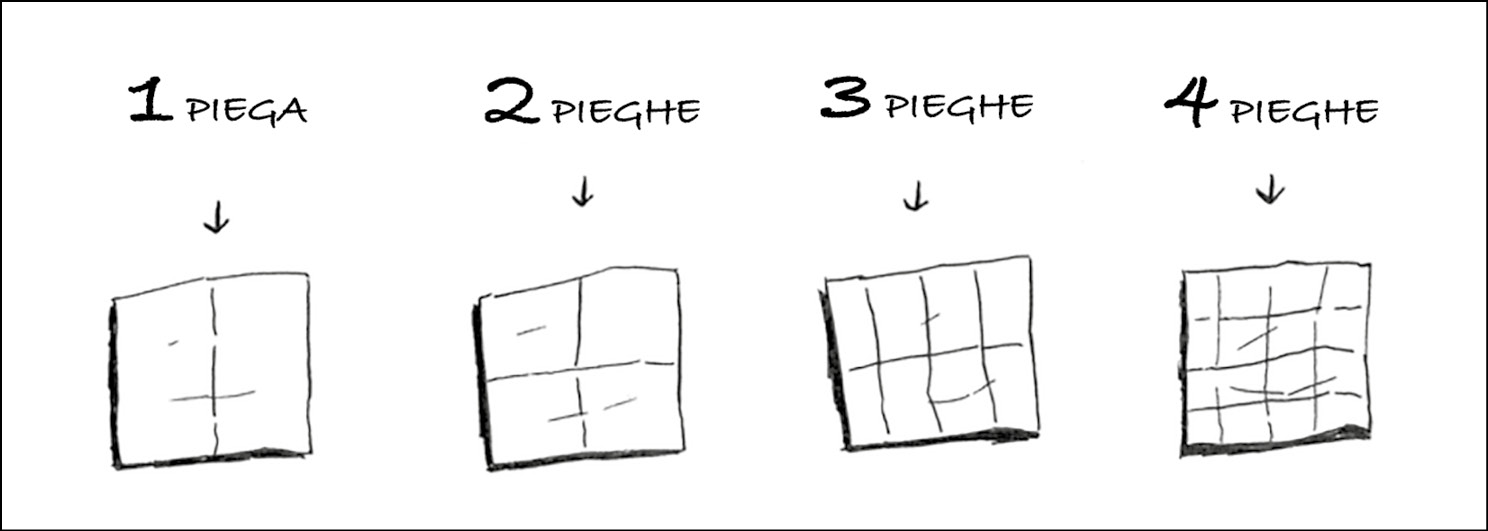
Proviamo invece questo algoritmo. Pieghiamo la carta in due.
Piegare la carta vale una operazione. Abbiamo appena realizzato due caselle con una sola operazione!
Leggi anche: 5 risposte su… scoprire gli algoritmi essenziali per la programmazione
Pieghiamo in due la carta ancora, e poi ancora e ancora.
Apriamo il foglio dopo quattro pieghe e avremo una bellissima griglia! Ogni piega raddoppia il numero di caselle. Abbiamo realizzato 16 caselle con 4 operazioni!
Disegnare una griglia in quattro pieghe.
Qual è il tempo di esecuzione di questo algoritmo? Troviamo i tempi di esecuzione per entrambi gli algoritmi, prima di procedere.
Risposte: l’algoritmo 1 impiega O(n) e l’algoritmo 2 impiega O(log n).
Alcuni tempi Big O comuni
Ecco cinque tempi di esecuzione Big O che incontreremo molto spesso, ordinati dal più veloce al più lento.
- O(log n), noto anche come tempo logaritmico. Esempio: la ricerca binaria.
- O(n), noto anche come tempo lineare. Esempio: la ricerca semplice.
- O(n
*log n). Esempio: un algoritmo di ordinamento veloce, come quicksort. - O(n2). Esempio: un algoritmo di ordinamento lento, come selection sort.
- O(n!). Esempio: un algoritmo davvero lento, come quello del commesso viaggiatore (nella prossima risposta).
Tempi di disegno di una griglia per alcuni algoritmi comuni.
Perché alcuni algoritmi non hanno (ancora) una soluzione certa
Il commesso viaggiatore
Ecco un esempio di un algoritmo con un tempo di esecuzione davvero pessimo. Questo è un problema famoso, perché la sua crescita è spaventosa e molte persone molto intelligenti pensano che non possa essere migliorato. Si chiama problema del commesso viaggiatore.
Abbiamo un venditore.
Il venditore deve andare in cinque città.
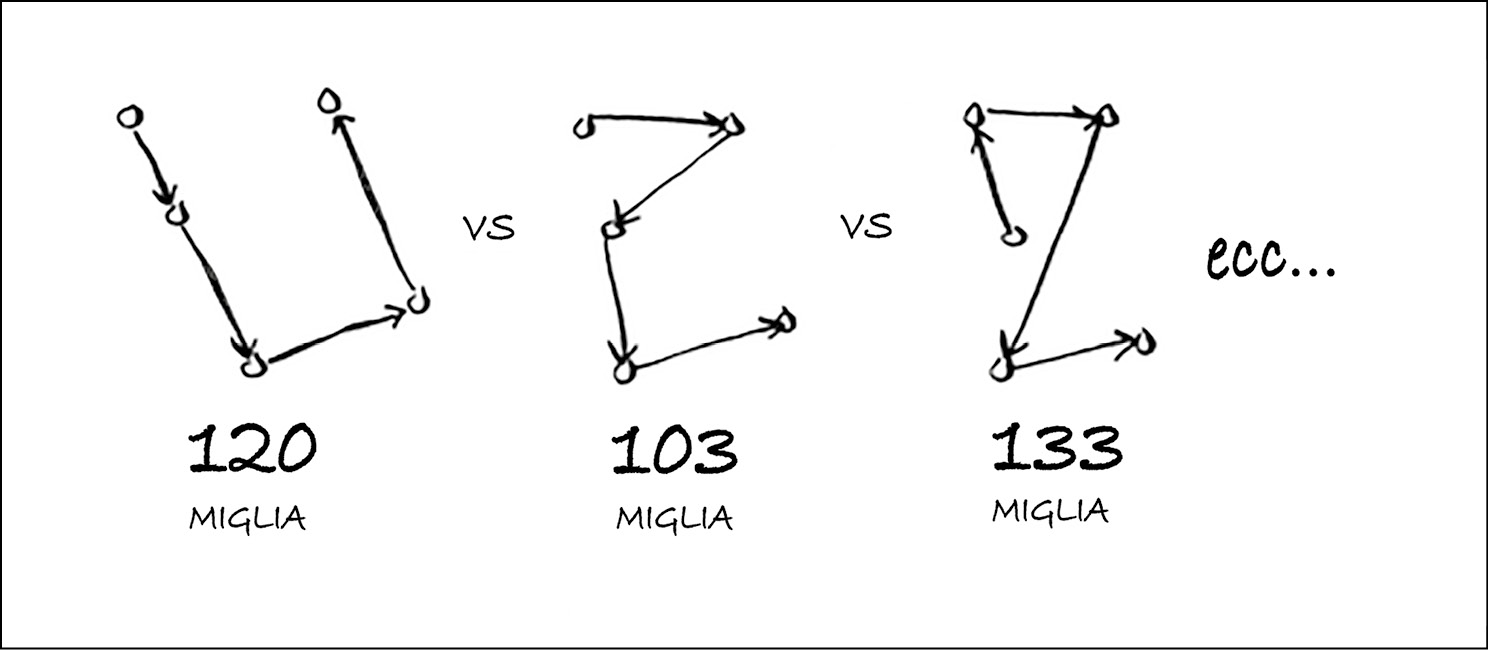
Questo venditore, che chiamerò Opus, vuole raggiungere tutte e cinque le città percorrendo la distanza minima. Ecco un modo per farlo: considerare ogni possibile ordine in cui potrebbe visitare le città.
Somma le distanze, calcola i totali e poi sceglie il percorso più breve. Cinque città danno 120 permutazioni, quindi ci vorranno 120 operazioni per risolvere il problema, per cinque città. Per sei città, ci vorranno 720 operazioni (per 720 permutazioni). Per sette città, ci vorranno 5.040 operazioni!
Il numero di operazioni aumenta drasticamente.
In generale, per n elementi, ci vorranno n! (n fattoriale) operazioni per calcolare il risultato. Quindi questo è un tempo O(n!), o tempo fattoriale. Occorrono molte operazioni per qualsiasi calcolo, tranne che per i numeri più piccoli. E se abbiamo a che fare con più di 100 città, diventerà impossibile calcolare la risposta in tempo: farà in tempo a spegnersi il Sole.
Questo è un algoritmo terribile! Opus dovrebbe usarne un altro, giusto? Ma non può. Questo è uno dei problemi irrisolti dell’informatica. Non esiste un algoritmo veloce per risolvere questo problema, e molti pensano che sia impossibile trovarlo. Il meglio che possiamo fare è trovare una soluzione approssimativa. Un’ultima nota: chi conosce l’argomento, provi con gli alberi binari!
Perché gli algoritmi ricorsivi fanno girare la testa
La ricorsione è una tecnica di programmazione utilizzata da molti algoritmi, elegante e divisiva. C’è chi la ama e chi la odia (o, per lo meno, la odia fintantoché non la capisce, poi la ama). Personalmente, appartenevo a questo terzo gruppo. Per semplificare le cose, ho un consiglio.
Almeno una volta, svolgiamo a mano una funzione ricorsiva, con carta e penna: qualcosa come Vediamo, passo 5 a factorial e restituisco 5 moltiplicato per quel che ottengo passando 4 a factorial, il quale a sua volta… e così via. Questo piccolo esercizio ci insegnerà come si comporta una funzione ricorsiva.
La ricorsione in pratica
Supponiamo di curiosare nella soffitta della nonna e di imbatterci in una misteriosa valigia chiusa a chiave.
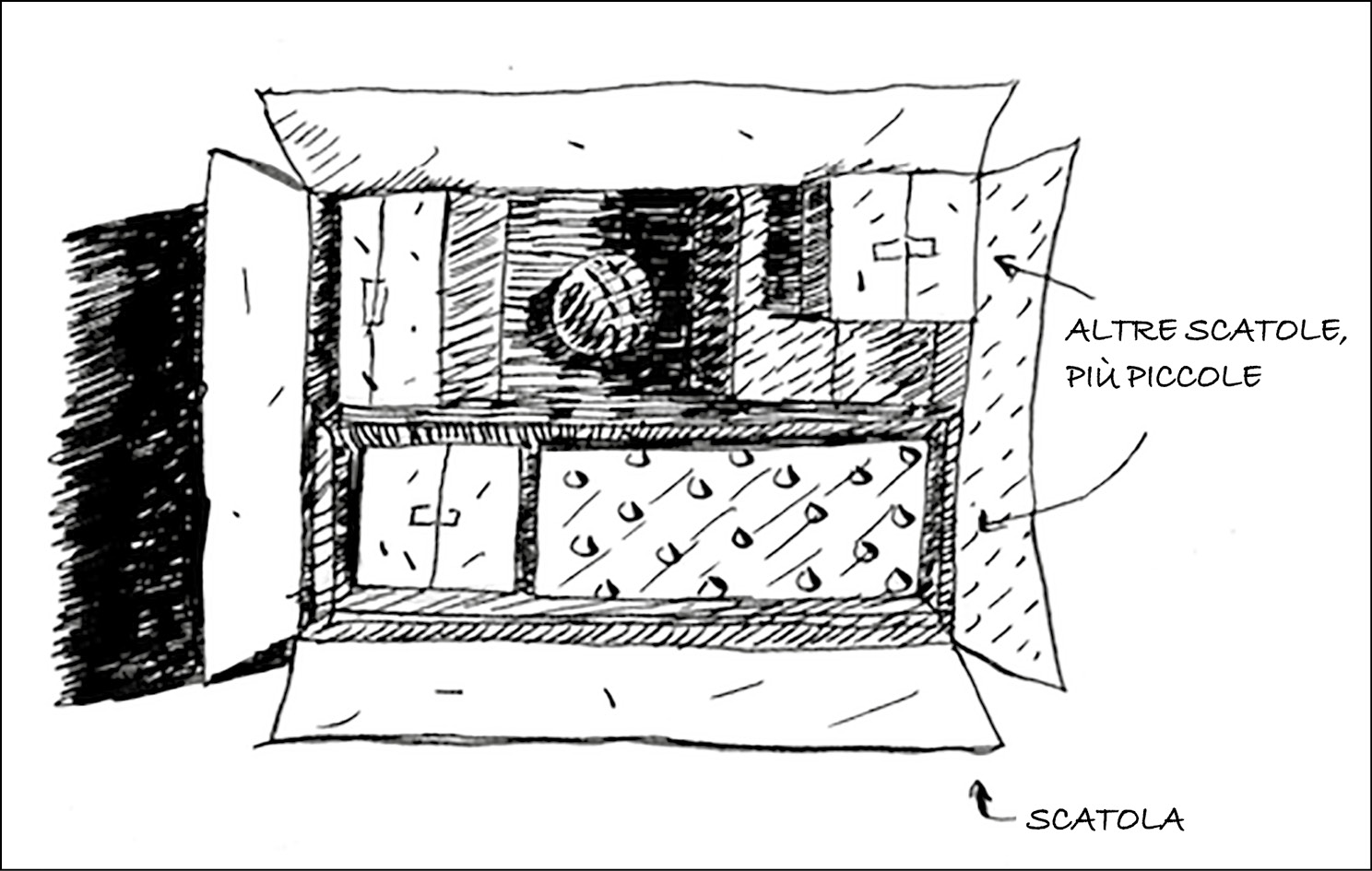
La nonna dice che probabilmente la chiave della valigia si trova in quest’altra scatola.
Questa scatola contiene altre scatole, le quali, a loro volta, contengono ulteriori scatole. La chiave è in una di queste scatole. Quale potrebbe essere il nostro algoritmo per cercare la chiave? Elaboriamo un nostro algoritmo prima di continuare a leggere.
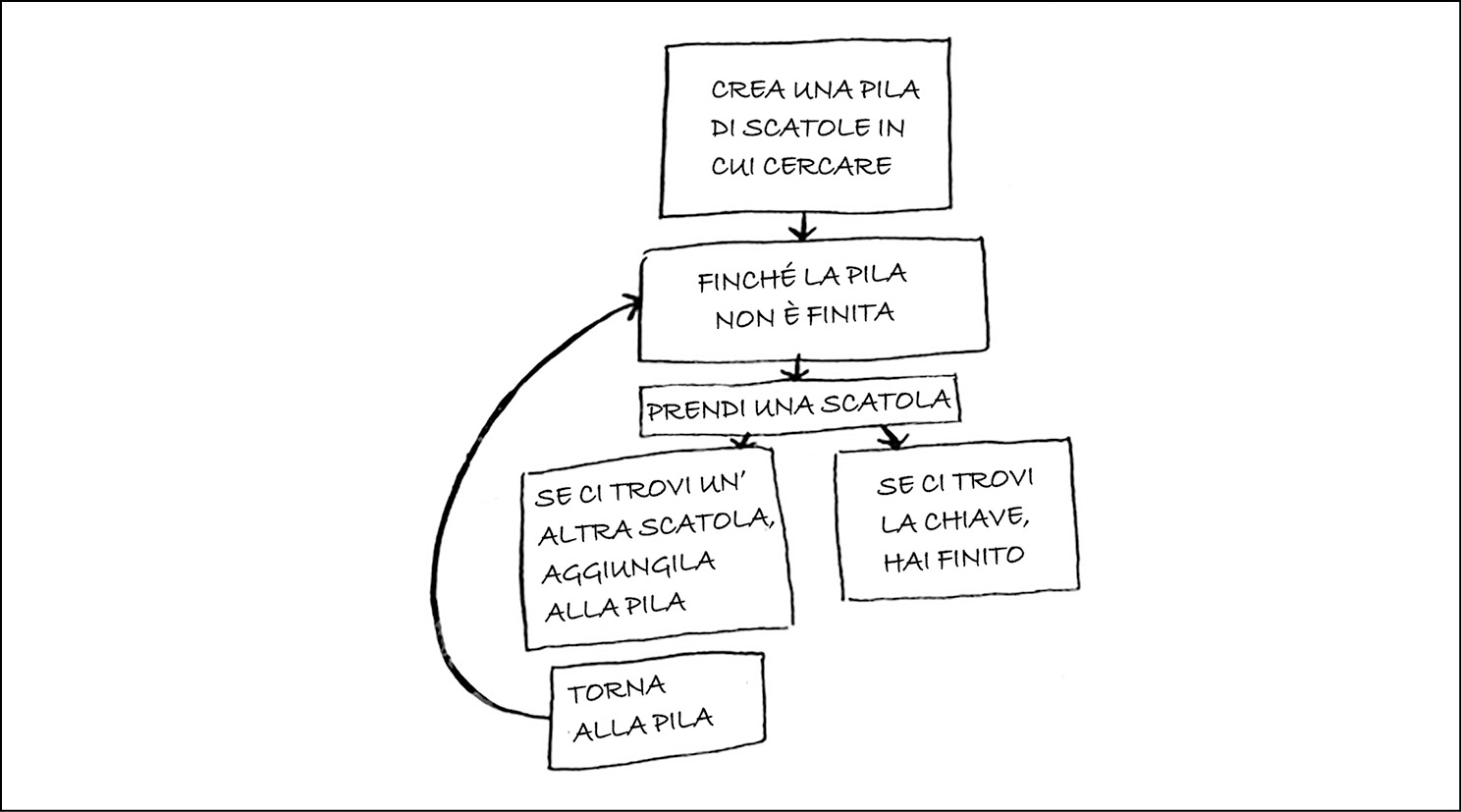
Ecco un approccio.
- Crea una pila di scatole in cui cercare.
- Prendi una scatola e guardaci dentro.
- Se trovi una scatola, aggiungila alla pila.
- Se trovi la chiave, il gioco è fatto!
- Ripeti.
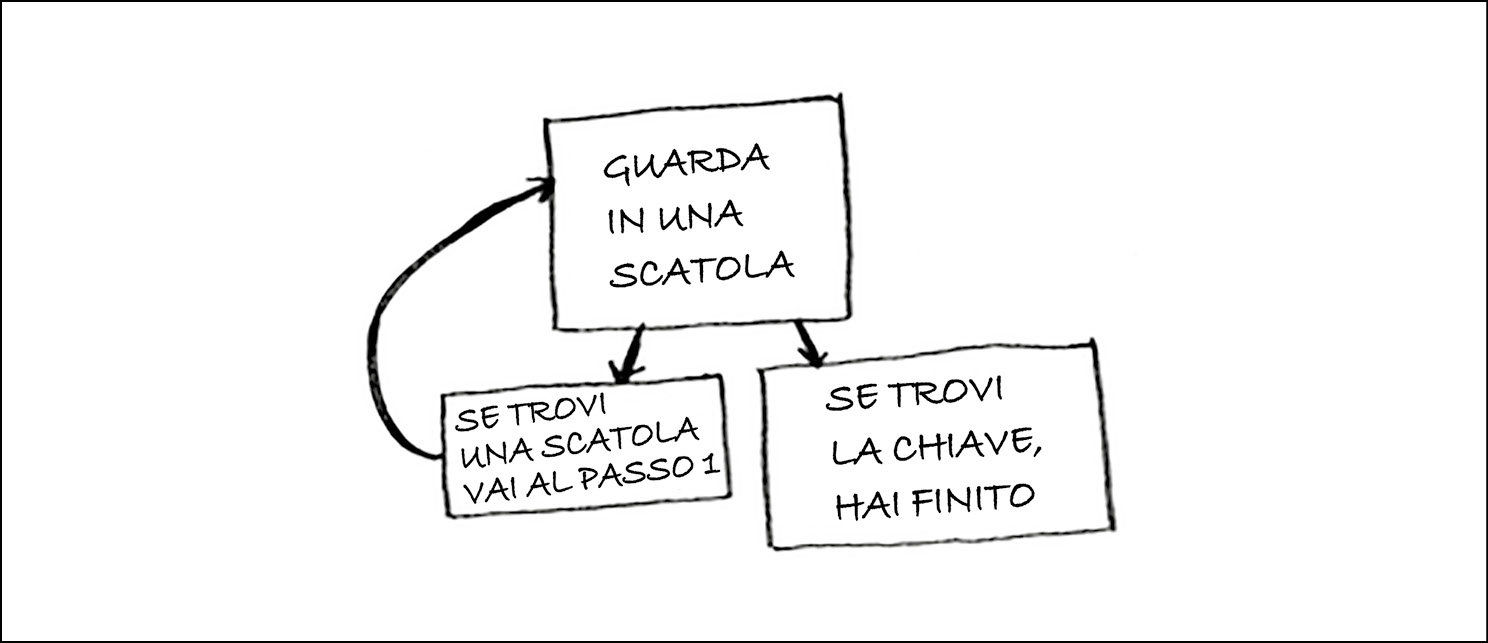
Ecco un approccio alternativo.
- Guarda in una scatola.
- Se trovi una scatola, vai al passo 1.
- Se trovi la chiave, il gioco è fatto!
Quale approccio sembra più facile? Il primo utilizza un ciclo while. Fintantoché la pila contiene scatole, prendiamo una scatola e ci guardiamo dentro:
def look_for_key(main_box):
pile = main_box.make_a_pile_to_look_through()
while pile is not empty:
box = pile.grab_a_box()
for item in box:
if item.is_a_box():
pile.append(item)
elif item.is_a_key():
print "Trovata la chiave"
Il secondo approccio, invece, utilizza la ricorsione. Nella ricorsione, una funzione richiama se stessa. Ecco il secondo modo in pseudocodice:
def look_for_key(box):
for item in box:
if item.is_a_box():
look_for_key(item) ➊
elif item.is_a_key():
print "Trovata la chiave!"
➊ Ecco la ricorsione.
Entrambi gli approcci fanno la stessa cosa, ma il secondo approccio è più chiaro. La ricorsione viene utilizzata quando semplifica la soluzione. Non c’è alcun vantaggio prestazionale legato all’uso della ricorsione; in realtà, a volte i cicli sono migliori in termini di prestazioni. Mi piace questa citazione di Leigh Caldwell su StackOverflow:
I cicli possono migliorare le prestazioni del programma. La ricorsione può migliorare le prestazioni del programmatore. Scegli il fattore più importante nella tua situazione!
Vi sono molti algoritmi importanti che usano la ricorsione, quindi è importante comprendere questo concetto.
Come funzionano gli alberi binari dentro gli algoritmi
Torniamo alla ricerca binaria. Quando un utente accede a Facebook, Facebook deve scartabellare un grosso array per scoprire se quel nome-utente esiste. Sappiamo che il modo più veloce per cercare in un array è eseguire una ricerca binaria. Ma c’è un problema: ogni volta che si iscrive un nuovo utente, ne inseriamo il nome-utente nell’array. Quindi dobbiamo riordinare l’array, perché la ricerca binaria funziona solo con array ordinati. Non sarebbe bello se potessimo inserire subito il nome-utente nella casella giusta dell’array, in modo da non doverlo ordinare in seguito? Questa è l’idea alla base della struttura ad albero binario.
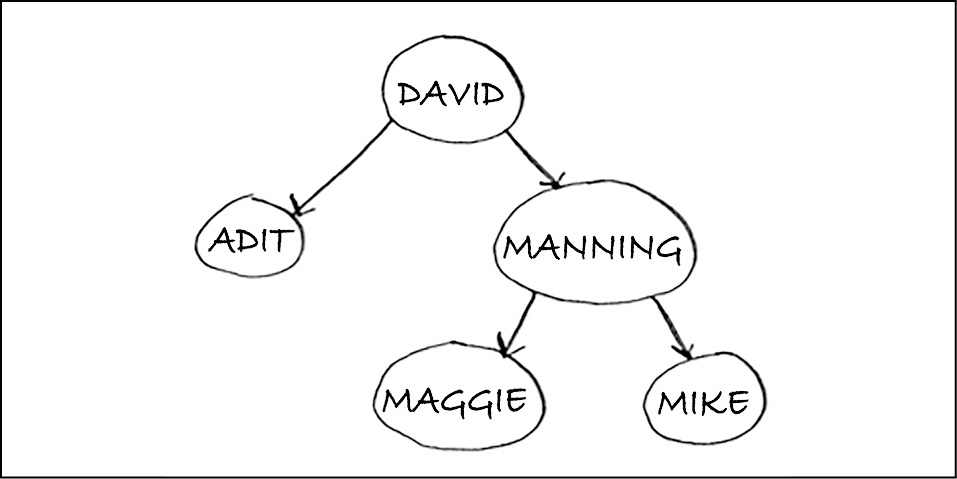
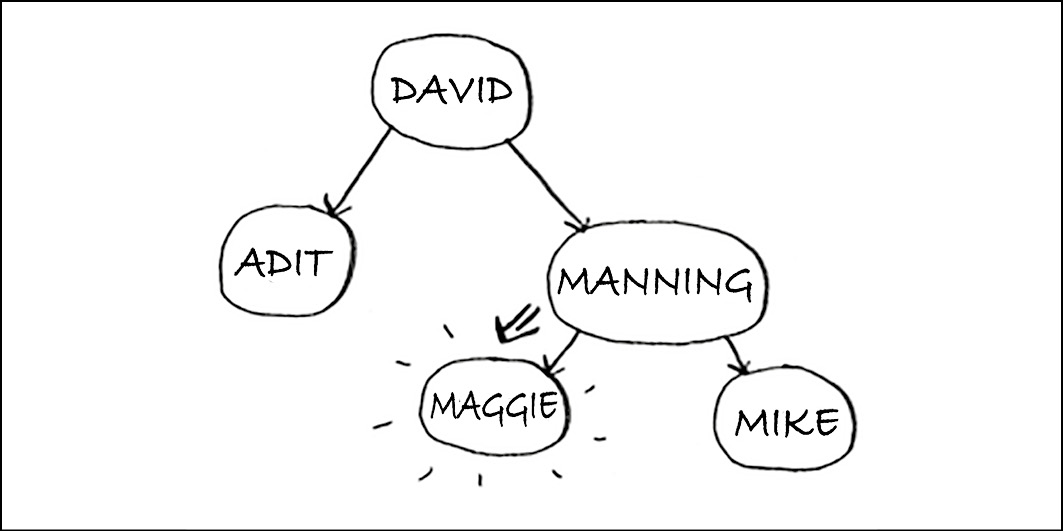
Un albero binario è simile a questo.
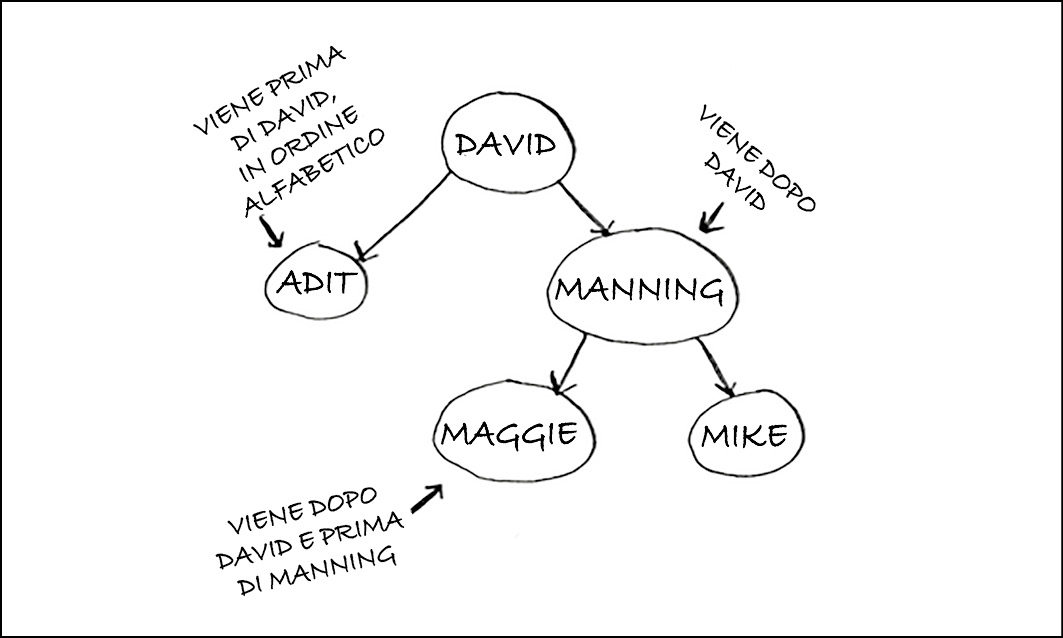
Per ogni nodo, i nodi alla sua sinistra hanno un valore inferiore e i nodi alla sua destra hanno un valore maggiore.
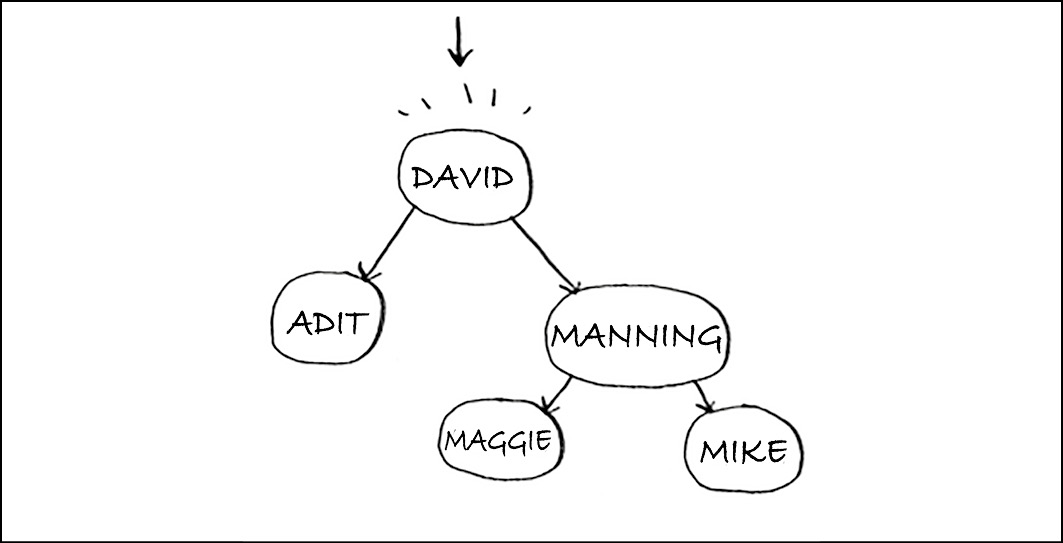
Supponiamo di voler cercare Maggie. Iniziamo dal nodo radice.
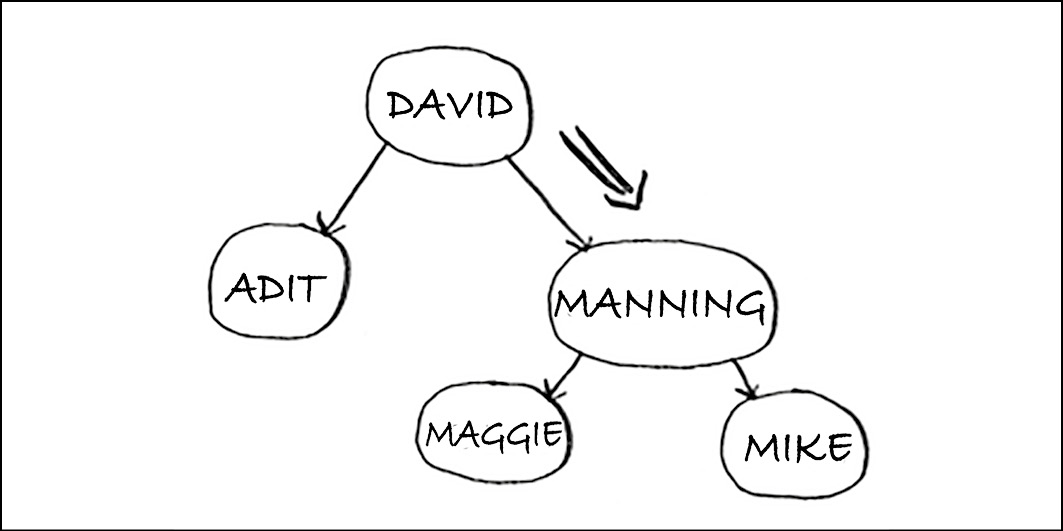
Maggie viene dopo David, quindi andiamo verso destra.
Ma Maggie viene prima di Manning, quindi andiamo verso sinistra.
Abbiamo trovato Maggie! È quasi come eseguire una ricerca binaria! La ricerca di un elemento in un albero binario richiede in media un tempo O(log n) e, nel caso peggiore, O(n). La ricerca in un array ordinato richiede un tempo O(log n) nel caso peggiore, quindi potremmo pensare che un array ordinato sia migliore. Ma un albero binario è in media molto più veloce per gli inserimenti e le eliminazioni.
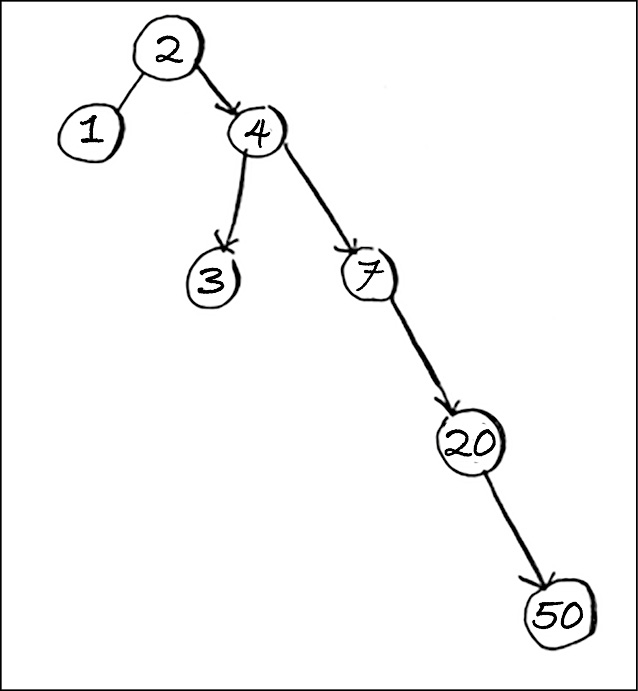
Gli alberi binari hanno anche alcuni aspetti negativi: innanzitutto, non offrono un accesso diretto. Non ha senso dire: Dammi il quinto elemento di questo albero. Anche i tempi delle prestazioni valgono in media e dipendono dall’equilibrio dell’albero. Supponiamo di avere un albero sbilanciato, come quello mostrato di seguito.
Si vede come è inclinato a destra? Questo albero non offre buone prestazioni, perché non è equilibrato. Esistono speciali alberi binari che si autobilanciano. I B-tree, un tipo speciale di albero binario, sono comunemente usati per memorizzare i dati nei database.
Chi avesse un interesse nei database o nelle strutture di dati più avanzate, può approfondire i seguenti argomenti.
Questo articolo richiama contenuti da Algoritmi spiegati in modo facile.