5 risposte su… Data Analysis & Visualization

Le 5 risposte

1. Come evitare l’insidia di Dio e della falsificabilità
2. Come si interpolano correttamente i dati
3. Perché fare attenzione ai campionamenti
4. Motivi per usare le estrapolazioni con cautela
5. Le ragioni per rinunciare al dogmatismo dei dati

1. Come evitare l’insidia di Dio e della falsificabilità

L’enunciato Dio esiste non appartiene al campo della scienza o dell’analisi dei dati. Qualsiasi cosa facciamo, non potremo mai dimostrarlo falso. Per questo mi dà fastidio quando qualcuno usa la scienza o i dati per cercare di confutare l’esistenza di una divinità. Possiamo crederci oppure no. Se non ci crediamo, però, non illudiamoci di possedere le prove che un Dio non esiste.

D’altra parte, se ci crediamo, non andiamo in giro a proporre una serie di enunciati a loro volta non falsificabili su come un dio abbia creato l’universo, chiamandoli scienza, perché scienza non sono.

Questa è la duplice natura di quella che chiamo l’insidia di Dio nell’analisi dei dati: o formiamo un’ipotesi non falsificabile, o facciamo tutto quello che possiamo per proteggere la nostra ipotesi da ogni possibile tentativo di dimostrarne la falsità.

Se ci pensiamo, dovremmo in realtà provare più entusiasmo per i dati che dimostrano come le verità universali che abbiamo adottato siano false e richiedano un aggiornamento. I grandi salti nella conoscenza avvengono quando ci rendiamo conto di esserci completamente sbagliati.

Sarebbe bello se fossimo fatti così, ma semplicemente non lo siamo. La realtà così fa breccia continuamente nelle nostre illusioni, rende chiari i nostri errori epistemici e ci rendiamo conto di essere ancora caduti in una trappola.

Un esempio: passaggi di biciclette

Come si evita di cadere in queste due trappole epistemiche? Cominciamo prendendo in esame il processo che ci mette nei guai. Ecco come si svolge questo processo, e il nostro modo di pensare:

1. Domanda di base → 2. Analisi dei dati → 3. Enunciato singolare → {non ci rendiamo conto del salto induttivo} → 4. Credenza in un enunciato universale.

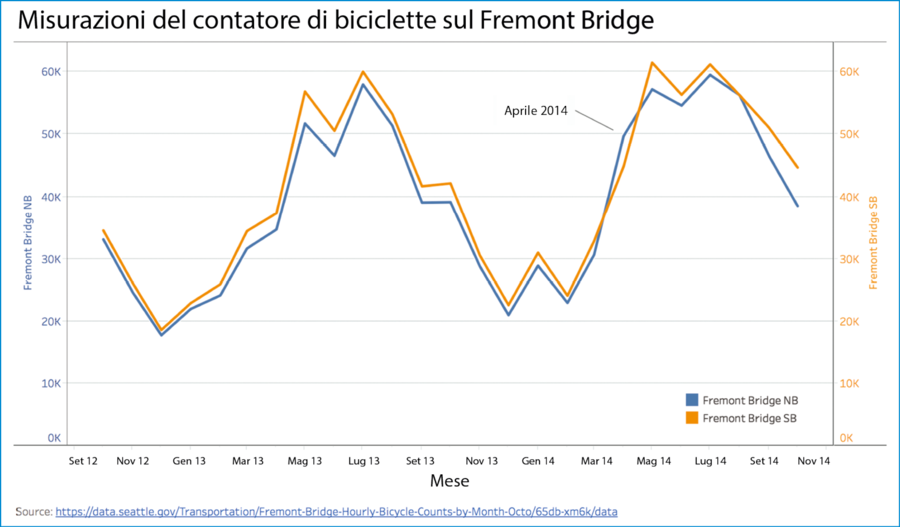
Per esempio, vediamo come sia andata nel caso del conteggio delle biciclette che passavano sul Fremont Bridge.

1. Ho saputo che c’è un contatore delle biciclette sul Fremont Bridge.
2. Ho trovato un po’ di dati forniti dall’Ufficio dei trasporti di Seattle, e sembra che…
3. 49.718 biciclette hanno attraversato il ponte in direzione est e 44.859 lo hanno attraversato in direzione ovest nell’aprile 2014.
4. Hmm, sono molte di più le biciclette che attraversano il ponte in direzione est. Come mai? Forse qualcuno attraversa il ponte per andare al lavoro il mattino in bici ma poi torna a casa in autobus.

L’evidenza del salto induttivo può essere individuata in qualcosa che può sembrare insignificante: un cambiamento nel tempo di un verbo. Ho messo i verbi in grassetto, in modo che fosse più facile coglierla. Nel passo 3, abbiamo parlato di biciclette che hanno attraversato il ponte (ossia, che sono state misurate e registrate). Nel passo 4, però, siamo passati al verbo presente e abbiamo usato attraversano. E subito siamo caduti vittima ancora una volta della trappola induttiva.

Propongo invece di procedere in questo modo:

1. Domanda di base → 2. Analisi dei dati → 3. Enunciato singolare → 4. Ipotetico enunciato universale falsificabile → 5. Un serio tentativo di confutarlo.

1. Quante biciclette attraversano il Fremont Bridge in un mese?
2. Ho trovato un po’ di dati dall’Ufficio dei trasporti di Seattle, e sembra che…
3. I dati fanno pensare che i contatori delle biciclette ne abbiano registrate 49.718 in direzione est e 44.859 in direzione ovest nell’aprile 2014.
4. Hmm, allora quel mese le apparecchiature hanno registrato più biciclette in direzione est che in direzione ovest. Mi chiedo: tutti i mesi sono state registrate più biciclette che andavano a est?
5. Vediamo un po’ se le cose sono andate diversamente.

Un’ulteriore analisi mostra che in effetti è stato un caso fuori dall’ordinario.

Misurazioni del contatore delle biciclette sul Fremont Bridge.

Va bene, dunque negli ultimi due anni sembra che la mia ipotesi fosse falsa: in genere il conteggio è maggiore per le bici che vanno verso ovest (Fremont Bridge SB) e minore per quelle che vanno verso est (Fremont Bridge NB) e posso vedere uno schema stagionale con numeri più elevati nei mesi estivi. Mi chiedo che cosa sia successo nell’aprile 2014 e dovrò guardare i dati successivi per vedere se la tendenza stagionale si mantiene o se le cose cambiano.

Si vede come sottili cambiamenti nel modo in cui pensiamo ai dati e nel modo in cui ne parliamo possano dare meno errori epistemici, migliori domande successive e una comprensione più accurata del mondo in cui viviamo. Si noti che sono stato attento a evitare di cadere nel divario fra dati e realtà, parlando del conteggio fornito dai contatori delle biciclette, invece che di biciclette che effettivamente attraversano il ponte.

Come sempre, il diavolo si nasconde nei dettagli. E per il diavolo contano molto i dettagli nel modo in cui pensiamo alle cose.

Torna all’inizio.

2. Come si interpolano correttamente i dati

Qualunque raccolta di dati in serie temporale comporta una decisione sulla frequenza di campionamento, cioè sul numero dei campioni raccolti in una data unità di tempo. Quanto spesso verranno raccolti i dati? Quanto tempo intercorrerà fra una misurazione e la successiva? Quando analizziamo o visualizziamo i dati, su quale livello di aggregazione baseremo la nostra indagine?

Mostriamo quanto è importante lavorando su dati sull’aspettativa di vita nel mondo ricavati dalla World Bank, per illustrare quali conseguenze abbia questa scelta a scala macro: trattiamo i dati su base annua.

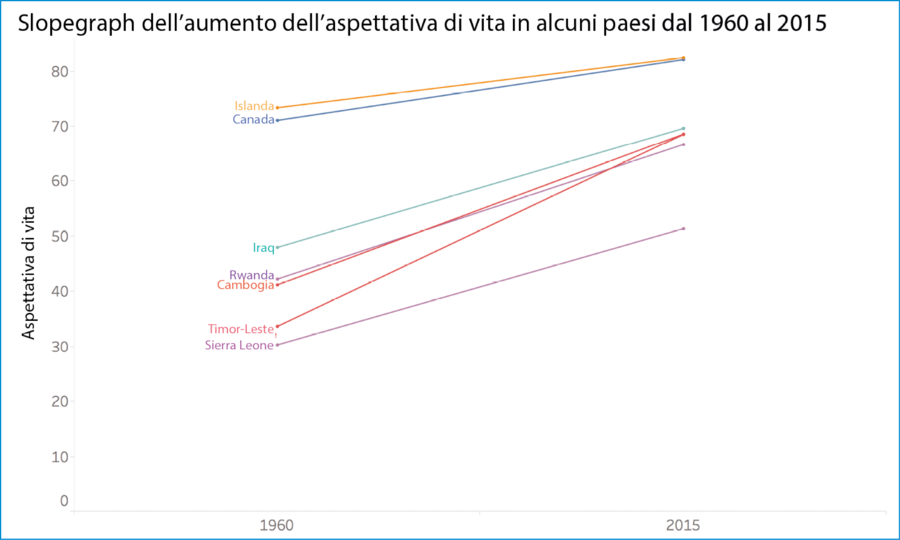
Lo slopegraph, o grafico a pendenza, è un modo molto diffuso per visualizzare i cambiamenti nel tempo. Se selezioniamo sette Paesi particolari e creiamo un grafico a pendenza in cui mostriamo come siano variate le aspettative di vita in ciascuno, dal 1960 al 2015, otteniamo una rappresentazione come quella in figura.

Grafico a pendenza dell’aumento dell’aspettativa di vita.

Se ci pensiamo, abbiamo appena creato un numero infinito di nuovi punti, del tutto fittizi: quelli che giacciono sul segmento disegnato fra i due valori. E che cosa ricaviamo, fondamentalmente, da questa costruzione? In tutti i paesi l’aspettativa di vita è aumentata, dal 1960 al 2015. Non è un’affermazione sbagliata, d’altro canto: è un semplice fatto. Ma è un’affermazione terribilmente incompleta.

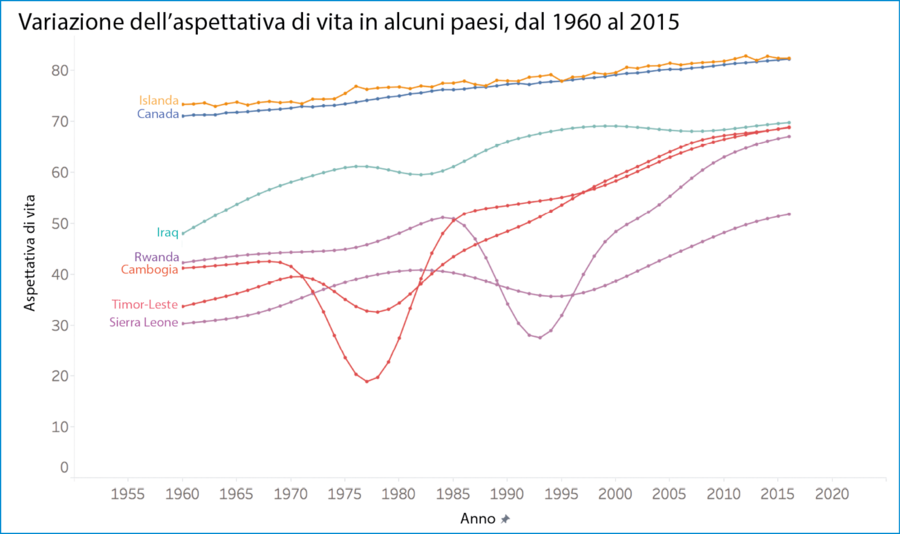
Vediamo che cosa succede se inseriamo i valori annuali in mezzo ai due anni estremi: oltre mezzo secolo di dati sull’aspettativa di vita. Come cambia la nostra storia? Così.

Come è cambiata l’aspettativa di vita nel corso degli anni.

Questa rappresentazione racconta una storia molto diversa, vero? Non mancano più i periodi tragici delle guerre in Cambogia, Timor-Leste, Sierra Leone e Rwanda. Sì, questi paesi hanno visto aumenti notevoli dell’aspettativa di vita nel corso dei 55 anni indicati qui, ma per arrivare a questo punto hanno dovuto superare enormi bagni di sangue. In Cambogia l’aspettativa di vita è scesa sotto i 20 anni d’età nel 1977 e 1978, l’anno in cui sono nato io. Il grafico a pendenza fallisce miseramente, poiché omette completamente questi aspetti. Non si avvicina neanche a raccontarci tutta la storia.

Anche quello dell’Iraq è un caso interessante. La parte della storia che manca nel grafico a pendenza è che l’aspettativa di vita in quel paese non è sostanzialmente variata dalla metà degli anni Novanta. I bambini nati in Iraq nel 1995 potevano aspettarsi di vivere fino a 68 o 69 anni, e lo stesso si può dire per i bambini nati in quel paese nel 2015. Due decenni di stagnazione. Nel grafico a pendenza non si vede.

Infine, il confronto fra Canada e Islanda è tecnico, ma comunque interessante. Nel grafico a pendenza, sembra che seguano più o meno lo stesso andamento. Ed è vero, ma se si confrontano i dati nella cronologia completa, si vede che la linea dell’Islanda va un po’ a zig-zag, con molto rumore da un anno all’altro, mentre la linea del Canada è molto più regolare. Che cosa succede qui? Non sono sicuro, ma posso supporre che abbia qualcosa a che vedere con il modo in cui ciascun Paese stima e pubblica ogni anno l’aspettativa di vita, e forse anche con la dimensione della popolazione di ciascun Paese. Chiaramente, hanno procedure diverse, modi diversi di calcolare e stimare questa metrica, metodi diversi.

È importante? Forse sì, forse no. Dipende dal tipo di confronto che si vuole effettuare. Sicuramente è interessante notare che esistono chiaramente molti modi diversi per ottenere la serie temporale di ciascun paese. L’elemento principale che volevo evidenziare è che, se si sceglie una frequenza di campionamento bassa, questi aspetti si possono perdere completamente.

Torna all’inizio.

3. Perché fare attenzione ai campionamenti

A qualche livello, sappiamo tutti che i dati che usiamo per trarre conclusioni sul mondo non sono perfetti. Dai risultati dei sondaggi agli studi clinici, per arrivare ai ponti degli ingegneri, c’è sempre qualche errore nei calcoli. Tendiamo a trascurare questa incertezza e la conseguenza è che portiamo fuori strada noi stessi e gli altri.

Un esempio: le etichette dei pesci

Quando un’organizzazione no profit nel febbraio 2013 ha pubblicato i risultati di un’inchiesta sulle frodi nell’etichettatura di pesce e frutti di mare, le conclusioni erano sconvolgenti: oltre 1.200 campioni di animali marini, raccolti da 674 dettaglianti in 221 Stati evidenziavano una tendenza inquietante, oltre il 33 percento dei campioni di DNA non corrispondevano alla specie dichiarata.

Un salto inferenziale

Seattle e Portland sono fra le migliori città del Paese in cui acquistare pesce etichettato accuratamente, sosteneva un articolo pubblicato dalla Northwest Public Radio (oggi non più disponibile sul suo sito).

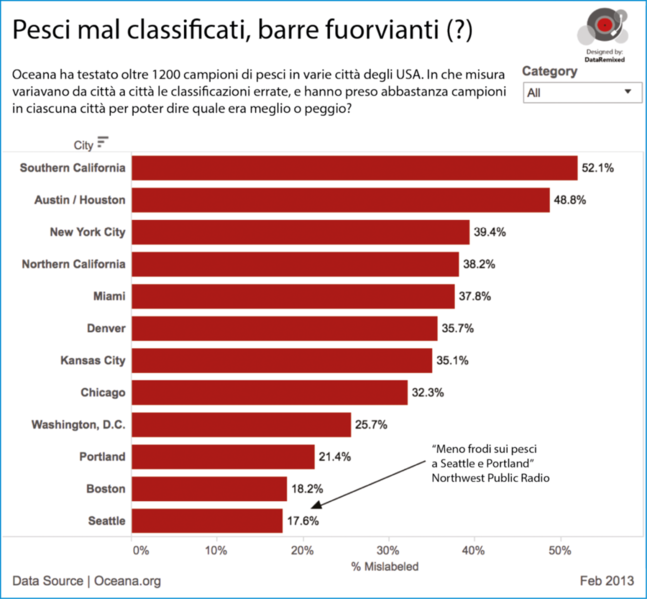
Per divertimento, ho pensato di dare uno sguardo più approfondito e ho trovato online il report completo. Vediamo dal report che cosa si può dire di Seattle e Portland. I grafici che seguono sono stati creati da me a partire dai dati grezzi forniti dal report.

Se consideriamo solo le percentuali dei campioni mal classificati per le varie città, troviamo Seattle e Portland tra le migliori, accanto a un altro centro importante per la pesca come Boston.

Se questo fosse tutto quello che abbiamo, trarremmo le stesse inferenze della Northwest Public Radio. Ma i campioni sono stati raccolti correttamente?

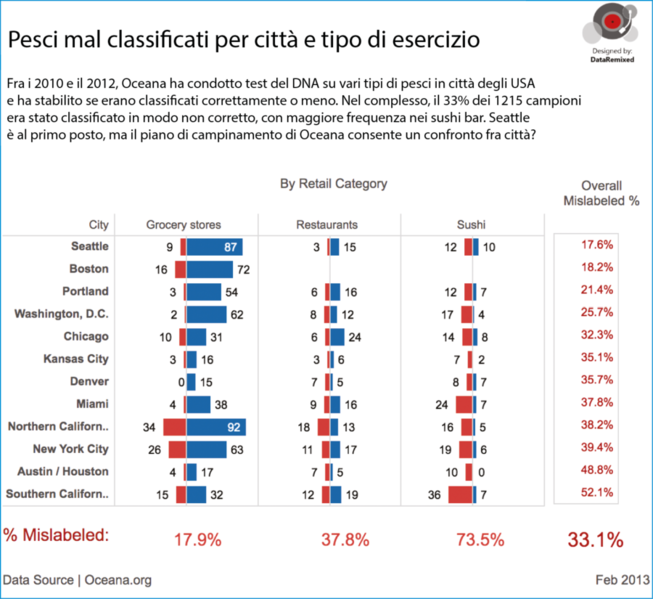
I campioni sono stati raccolti da tre tipi di esercizi: negozi di alimentari, ristoranti e sushi bar. Nella prossima figura sono riportati i risultati per ciascuna città e per i relativi tipi di esercizi. I campioni mal classificati sono le barre in rosso, quelli classificati correttamente le barre in blu.

Le classificazioni errate dei pesci per città e tipo di esercizio.

La prima cosa che ho notato è che le dimensioni dei campioni sono molto piccole, una volta che si disaggregano i dati per città e tipo di esercizio. Sì, potranno anche esserci più di 1200 campioni nel complesso, ma 12 campioni dai ristoranti nell’area Austin/Houston? E 9 campioni dai sushi bar di Kansas City?

I sushi bar sembrano dare i risultati più scarsi, con oltre il 73% di pesci mal classificati fra tutte le città.

L’altra cosa che si nota è che nelle varie città sono stati raccolti campioni molto diversi di sushi. A Boston addirittura non è stato raccolto neanche un campione.

Scomposizione

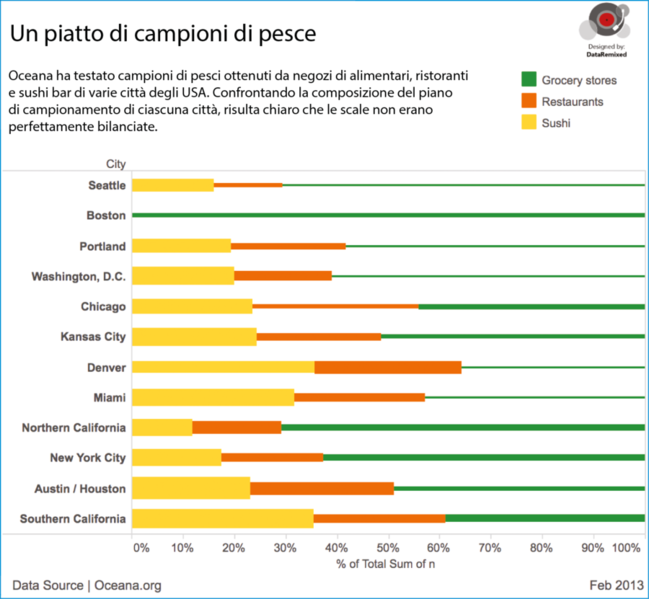
La prossima figura mostra una scomposizione dei totali per ciascuna categoria di esercizi nel campione di ciascuna città (lo spessore delle barre è proporzionale al numero dei campioni mal classificati: barre più spesse corrispondono a un tasso di classificazioni errate più elevato).

Composizione dei campioni di pesci.

Quindi, a Seattle, Portland e Boston sono stati raccolti campioni relativamente poco numerosi dai sushi bar. Dei campioni di Seattle, il 16% veniva da sushi bar, mentre oltre il 35% dei campioni della California meridionale veniva da questo tipo di esercizi, per fare un esempio.

L’organizzazione non ha seguito un piano di campionamento stratificato, quando ha raccolto i suoi 1214 campioni e di conseguenza i tassi complessivi dei pesci mal classificati per ciascuna città non sono correttamente confrontabili. Questo non vuol dire che lo studio non abbia senso; significa solo che i confronti fra i tassi complessivi di ciascuna città non sono validi. Sarebbe come confrontare l’altezza media degli abitanti delle varie città, includendo nel campione di una città più bambini che nei campioni delle altre. Non sarebbe un confronto alla pari.

Confrontare il simile con il simile

Se non possiamo davvero confrontare i tassi complessivi, potremmo magari comparare le città per categoria di esercizio, negozi di alimentari con negozi di alimentari, ristoranti con ristoranti, sushi bar con sushi bar?

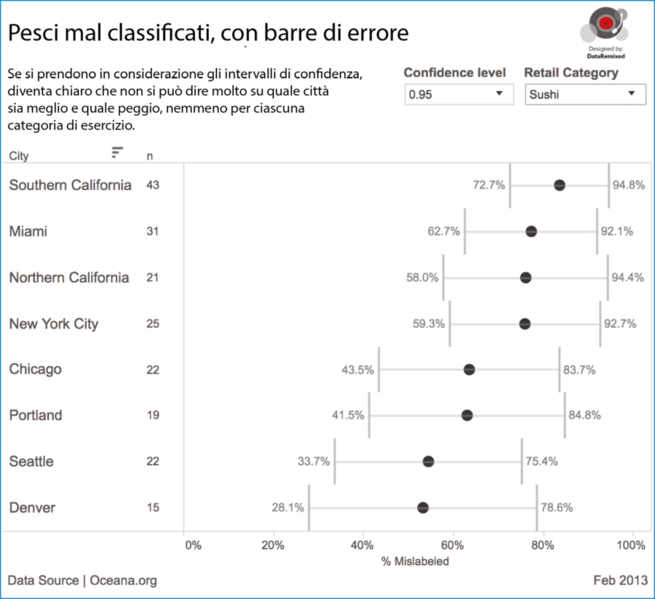
Anche se nel complesso è stato raccolto un numero relativamente elevato di campioni, la dimensione dei campioni diventa abbastanza piccola se si prende in considerazione ciascuna combinazione città/categoria, perciò dobbiamo aggiungere delle barre di errore ai tassi di cattiva classificazione. Qui dobbiamo parlare di intervallo di confidenza per la proporzione binomiale. Qui sotto vediamo i tassi di cattiva classificazione disaggregati, con la relativa incertezza.

Pesci mal classificati, con barre di errore.

Questa visualizzazione dei dati racconta una storia molto diversa. Notiamo che nel grafico non sono comprese tutte le città perché, in qualche caso, non c’erano abbastanza campioni da soddisfare i requisiti dell’approssimazione normale (n * p > 5 e n * (1 – p) > 5).

Che cosa possiamo (e non possiamo) dire delle diverse città, sulla base di un intervallo di confidenza del 95 percento?

• Non abbiamo abbastanza evidenze per dire se una città sia meglio o peggio delle altre, per la classificazione del sushi.
• C’è una probabilità elevata che i ristoranti di Chicago nel complesso abbiamo tassi inferiori di classificazione errata rispetto ai ristoranti nella California settentrionale.
• C’è una probabilità elevata che i negozi di alimentari di Seattle abbiano un tasso di cattiva classificazione minore rispetto sia alla California (meridionale e settentrionale) sia a New York.

Qualche confronto fra le città dunque si può fare, ma non molti. Alla fine, gli abitanti di Seattle possono consolarsi con il fatto che i pesci nei loro negozi di alimentari probabilmente sono classificati più precisamente che in California o a New York.

Se ci si può fidare dei test, e se questi possono essere replicati, questa organizzazione ha messo in luce quanto sia diffusa negli Stati Uniti una cattiva classificazione dei pesci: questo è innegabile. Ma chi ha riportato questa vicenda ne ha tratto un grosso salto inferenziale. Se si osservano i numeri attraverso la lente della statistica si possono formulare affermazioni più accurate su ciò che è stato raccolto.

Certo, questo comporta molto più lavoro rispetto semplicemente a prendere il tasso complessivo di cattiva classificazione e riportarlo su una mappa o un grafico a barre. E sì, l’incertezza può essere irritante, ma ci infiliamo in una trappola e inganniamo noi stessi e gli altri se non comprendiamo come il nostro piano di campionamento e gli intervalli di confidenza incidono sulla nostra possibilità di trarre conclusioni probabilistiche sul mondo in cui viviamo.

Abbracciare l’incertezza può voler dire fare la differenza fra verità e finzione e noi non vogliamo fare la figura di quelli che abboccano come pesci, vero?

Torna all’inizio.

4. Motivi per usare le estrapolazioni con cautela

Spesso si pensano gli “analytics” come l’applicazione di strumenti e tecniche per usare i dati al fine di prendere decisioni in merito al futuro. È una faccenda rischiosa e il processo analitico di previsione è pieno di pericoli e insidie. Questo non vuol dire che non dovremmo provarci, ma che dovremmo farlo con umiltà e un certo senso dello humor, con il radar per le insidie a pieno regime.

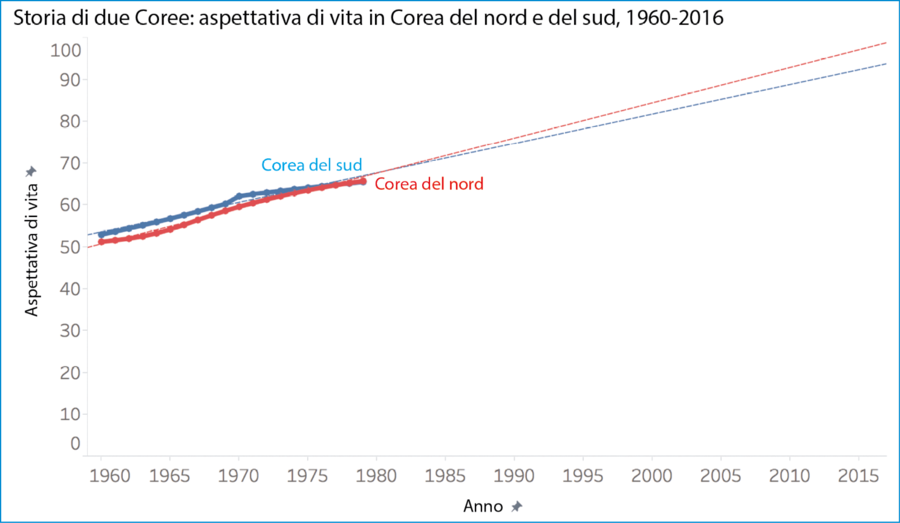
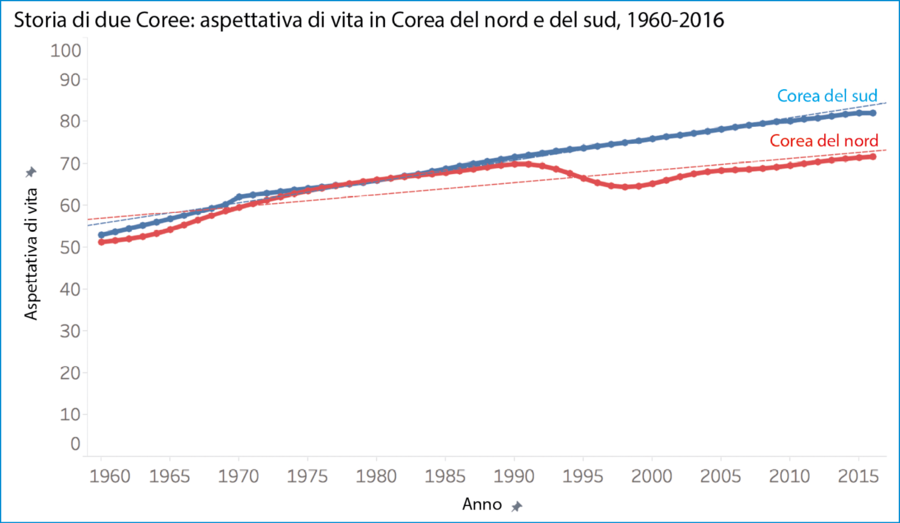
Per esempio, se consideriamo l’aspettativa di vita nella Corea del nord e del sud negli anni Sessanta e Settanta, vediamo che era di circa 50 anni intorno alla metà degli anni Sessanta. I nati in entrambi gli stati della penisola coreana negli anni Sessanta avvano una aspettativa di vita di circa 50 anni, quelli nati una quindicina di anni dopo avevano un’aspettativa di vita di circa 65 anni.

Storia di due Coree: aspettativa di vita in Corea del nord e del sud, 1960–2016.

Lo definisco un “incremento molto stabile”, perché le linee di regressione lineare per entrambi i paesi (linee tratteggiate nel grafico) hanno valori p minori di 0,0001 e coefficienti di determinazione, R^2, superiori a 0,95, il che significa che le variazioni nella variabile x (anno) spiegano una percentuale molto alta della variazione osservata nel valore y (aspettativa di vita). In altre parole, i punti di dati di ciascuna serie si avvicinano molto a formare una linea retta.

Se nel 1980 qualcuno si fosse basato esclusivamente sulla natura lineare di questa serie temporale di 20 anni per predire le aspettative di vita dei coreani che fossero nati 35 anni dopo, avrebbe individuato aspettative di vita di 96 anni per la Corea del nord e di 92 anni per la Corea del sud nell’anno 2015. Ovviamente, non è quel che vediamo realmente e non dovrebbe sorprendere nessuno. In primo luogo, l’aspettativa di vita della nostra specie non può aumentare indefinitamente. I dati finiranno per avvicinarsi a un tetto naturale, perché le persone non vivono per sempre. Se estendiamo la serie fino alla fine del nostro secolo, le persone nate nella penisola coreana potrebbero avere un’aspettativa di vita di circa 170 anni. Poco probabile, e nessuno lo sostiene.

Ma questo non è l’unico motivo per cui la previsione sarebbe stata di molto sbagliata. Diamo un’occhiata a come le linee di tendenza sono evolute nel corso degli ultimi 35 anni, per arrivare dove siamo oggi, con aspettative di vita di circa 82 anni per la Corea del sud e di circa 71 per la Corea del nord.

Storia di due Coree: aspettativa di vita nella Corea del nord e del sud, 1960–2016.

Mentre l’aspettativa di vita per i nati nella Corea del sud ha continuato ad aumentare in modo molto lineare (R^2 = 0,986), si può vedere che inizia a piegare verso il basso e ad assumere una forma non lineare mentre si avvicina a un asintoto.

Il caso della Corea del nord è molto diverso. Nella parte settentrionale della penisola si è verificato un cambiamento notevole e l’aspettativa di vita in reltà è diminuita di 5 anni nel corso degli anni Novanta, poiché gli abitanti di quel paese hanno dovuto fare i conti con una scarsa disponibilità di cibo e la mancanza di accesso ad altre risorse critiche. Chi poteva saperlo nel 1980?

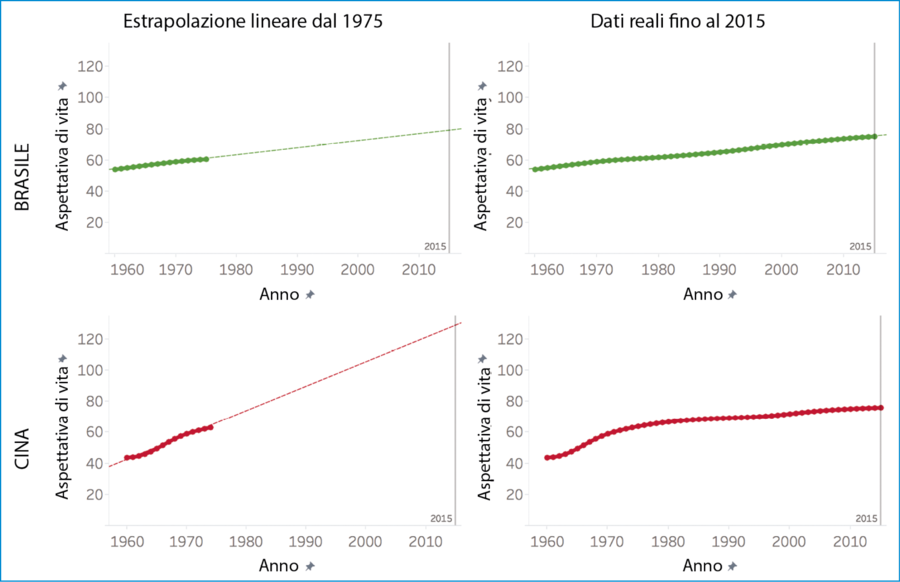
A volte le previsioni funzionano molto bene. Nel caso del Brasile, per esempio, l’aspettativa di vita ha continuato ad avere un andamento lineare sin dal 1960. Altre volte, però, non funziona affatto. Per la Cina, per esempio, un’estrapolazione lineare dal 1975 avrebbe dato una previsione improbabile di 126 anni di aspettativa di vita per i nati nel 2015. Ovviamente, i forti aumenti degli anni Sessanta non sono continuati e il dato 2015 reale è stato di 76 anni.

Estrapolazione lineare dal 1975.

Il caso dell’aspettativa di vita in Cina illustra come si debba stare molto attenti quando si adattano le equazioni ai dati empirici.

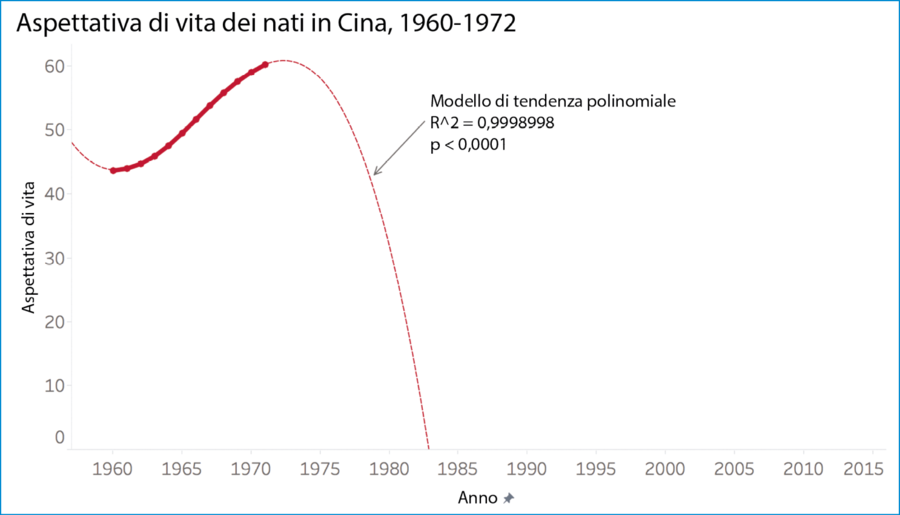
Riguardiamo la curva nella prossima figura, ingrandita in modo da vedere più in dettaglio la forma e il modello.

Non ci vuole un genio per stabilire che questo modello è ancora meno utile, per prevedere le aspettative di vita future, di un modello lineare. Produce una previsione del tutto priva di senso, con le aspettative di vita che crollano a 0 e addirittura diventano negative nell’arco di una quindicina d’anni.

È una fortuna per noi quando un modello che si adatta così bene ai dati si rivela del tutto bizzarro. È come se ci fosse una buca nella strada, ma ben segnalata da un enorme cartello di pericolo, davanti al quale lampeggiano luci intense. Se cadiamo in quell’insidia, vuol proprio dire che non stavamo prestando attenzione.

Aspettativa di vita per i nati in Cina, 1960-1972.

Torna all’inizio.

5. Le ragioni per rinunciare al dogmatismo dei dati

Come per altre forme di espressione e di comuniczione, non ci sono regole bianco e nero nella visualizzazione dei dati, solo regole empiriche. Non credo neanche che si possa mai dichiarare che un particolare tipo di visualizzazione funziona o non funziona in tutti i casi immaginabili.

A volte la scelta più efficace in una particolare situazione può sorprenderci. Consideriamo due campi apparentemente privi di relazioni con la visualizzazione dei dati: gli scacchi e la scrittura. La visualizzazione dei dati è simile agli scacchi poiché in entrambi i casi è coinvolto un numero enorme di mosse alternative.

Nella seconda analogia, la visualizzazione è come la scrittura, poiché entrambe comportano la comunicazione di pensieri ed emozioni complessi a un pubblico. Normalmente, quando si scrive per un lettore o un gruppo di lettori, valgono le regole comuni di ortografia, sintassi e grammatica. A scuola, gli studenti che violano queste regole ottengono pessimi voti, ma l’americano Cormac McCarthy, romanziere, autore di teatro e per il cinema, decise di fare praticamente a meno di ogni segno di interpunzione nel suo romanzo del 2006 La strada: nel 2007 ha vinto il premio Pulitzer per la narrativa con quel romanzo.

Consiglierei di prendere decisioni simili a chi è alle prime armi come giocatore di scacchi o come scrittore? No, ma nemmeno le eliminerei completamente dall’insieme di tutte le possibili soluzioni.

Dire a un aspirante giocatore di scacchi di non sacrificare mai una regina, o dire a uno scrittore alle prime armi di non tralasciare mai in nessun caso un punto o una virgola, non significa fargli un favore.

Certo non penso che vada sempre bene sacrificare la regina o omettere tutti i segni di interpunzione in un romanzo. Ogni tanto, però, queste cose sono proprio la soluzione perfetta.

Quanto è importante la libertà creativa

Mi fa molto piacere che ci siano tante persone creative e di talento nello spazio della visualizzazione dei dati, che provano nuove cose. La libertà di innovare è necessaria perché un campo possa svilupparsi a pieno; i pronunciamenti generalizzati su certi tipi di visualizzazioni invece non sono utili e tendono a ridurre lo spirito della libertà di innovare.

Innovazione non significa solamente creare nuovi tipi di grafici, ma anche usare i tipi di grafici già esistenti in modi nuovi e creativi, o applicare le tecniche correnti a nuovi insiemi di dati interessanti, o combinare la visualizzazione dei dati con altre forme di espressione, visuali o meno. Purché ci possa essere una discussione rispettosa ed educata su ciò che funziona e ciò che si potrebbe fare per migliorare l’innovazione, facciamoci sotto!

Aggiungere le idee vincenti allo spazio delle soluzioni note è un bene per tutti.

Questo articolo richiama contenuti da Data Analysis & Visualization.

Immagine di apertura di 小谢 su Unsplash.