L’estensione turtle di Python permette di scrivere programmi basati sulla geometria e sul piano cartesiano, che disegnano grazie a robot virtuali (o tartarughe digitali) istruiti a muoversi lasciando una traccia del percorso compiuto.
Primi passi
Nell’interprete di IDLE, l’ambiente più classico per partire con la programmazione Python, scrivi il seguente codice:
>>> import turtle
>>> ninja = turtle.Turtle() # Crea una "Turtle" di nome "ninja"
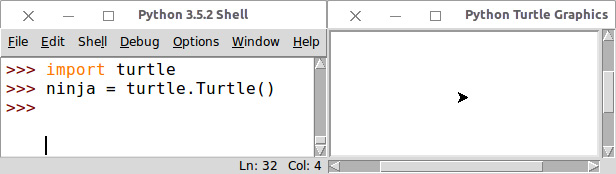
Dopo aver eseguito la seconda riga, appare una nuova finestra intitolata Python Turtle Graphics. Al centro di uno sfondo bianco, chiamato canvas, o tela, che rappresenta l’area di disegno, appare una tartaruga rappresentata dall’immagine di una punta di una freccia.
Affianca le due finestre come mostrato nella figura qui sotto; in questo modo puoi scrivere istruzioni nella finestra dell’interprete e contemporaneamente vedere il loro effetto nell’altra finestra.
La finestra dell’interprete Python affiancata alla finestra grafica di Turtle.
La seconda istruzione crea un oggetto di tipo Turtle, richiamando il suo costruttore (una specie di stampino) contenuto in turtle (attenzione: il nome del costruttore inizia con la maiuscola mentre quello del modulo è tutto minuscolo), e gli dà un riferimento, o un nome con cui chiamarlo, costituito dalla variabile ninja (un piccolo omaggio alla serie a fumetti e televisiva Tartarughe ninja, nata negli Stati Uniti nel 1984).
Ora fai muovere ninja con le seguenti istruzioni:
ninja.forward(100) # Procedi in avanti di 100 passi (o pixel)
ninja.left(90) # Ruota a sinistra, cioè in senso antiorario, di 90 gradi
ninja.forward(100) # Procedi in avanti di 100 passi (o pixel)
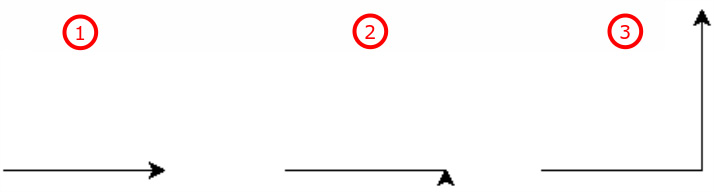
Quando si muove, ninja lascia una scia del percorso che compie (in effetti potevano chiamarla lumaca invece che tartaruga…). Osserva nella prossima figura il risultato dell’esecuzione dei singoli passaggi: la tartaruga può essere vista anche come una penna che, se è appoggiata al piano, vi scrive sopra.
La tartaruga, che andava a destra, va avanti, ruota di 90° e poi ancora avanti.
Analizziamo l’ambiente geometrico in cui si muove la tartaruga.
Come si muove Turtle
Un oggetto di tipo Turtle è caratterizzato da 3 attributi:
- una locazione, cioè la posizione in cui si trova sul piano;
- un orientamento, che indica la direzione in cui sta puntando;
- una penna, che ha a sua volta alcuni attributi come la dimensione, il colore, eccetera.
Per posizionare e muovere un oggetto su un piano, come il canvas di Turtle, è necessario avere un sistema di riferimento, così come nel gioco della Battaglia navale: per posizionare le navi, prima suddividi il foglio in una griglia rettangolare nella quale ogni cella è individuata da una coppia di coordinate (riga, colonna) a partire dall’angolo in alto a sinistra.
Coordinate x, y
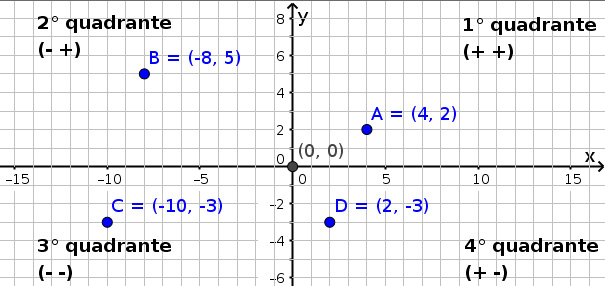
Turtle usa un sistema di riferimento ortogonale cartesiano simile a quello della battaglia navale. Le celle sono i singoli pixel (nella Figura 5.3 i pixel si trovano all’incrocio di una riga e una colonna). Gli assi x e y dividono l’area di disegno in 4 quadranti: il centro, da dove parte la tartaruga, ha coordinate (0, 0), l’ascissa x (coordinata orizzontale) cresce verso destra e l’ordinata y (coordinata verticale) cresce verso l’alto. Nella figura seguente sono riportati 4 punti di esempio, uno per ciascun quadrante: il punto A, nel 1° quadrante, ha entrambe le coordinate positive, il punto B, nel 2° quadrante, ha x negativa e y positiva eccetera.
La posizione della tartaruga è il pixel relativo alla punta della freccia.
Sistema di riferimento cartesiano di Turtle per il posizionamento sul canvas.
Direzione e rotazione
La direzione (heading) indica dove punta, o guarda, la tartaruga e determina il senso di marcia quando questa procede in avanti.
Per andare all’indietro (backward) è possibile utilizzare il corrispondente comando oppure procedere come il gambero, andando in avanti di una distanza negativa, cioè camminando all’indietro. Quindi, le due istruzioni seguenti sono equivalenti:
ninja.forward(-100) # Vai all'indietro di 100 pixel
ninja.backward(100) # idem (come sopra)
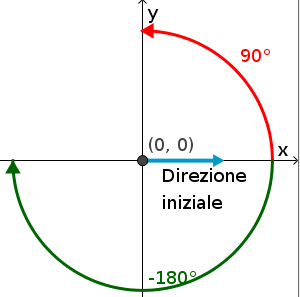
Per le rotazioni, di default gli angoli si misurano in gradi relativamente alla direzione corrente della tartaruga, che all’inizio punta verso destra (rappresentata dalla freccia azzurra nella figura qui sotto). Ruotando verso sinistra (left) la tartaruga gira in senso antiorario, ruotando verso destra (right) gira in senso orario.
È possibile anche utilizzare valori negativi per ruotare nel verso opposto. Quindi, le due istruzioni seguenti sono equivalenti:
ninja.left(-90) # Ruota in senso orario di 90°
ninja.right(90) # idem
Sistema di riferimento di Turtle per ruotare e cambiare la direzione di marcia.
Una scala colorata
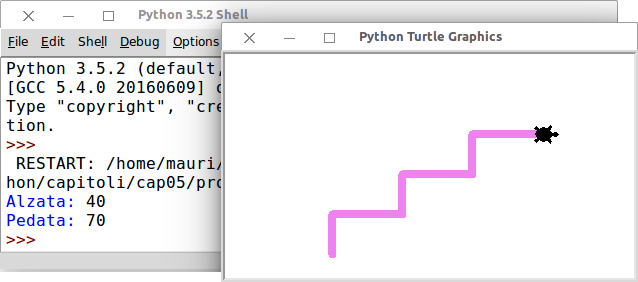
L’obiettivo è disegnare una scala colorata come mostrato nella figura che segue, chiedendo all’utente le misure del segmento verticale (o alzata) e del segmento orizzontale (o pedata). Poiché la funzione input() ritorna una stringa, è necessaria una conversione di quest’ultima in un valore numerico tramite la funzione eval().
Il listato mostra due nuovi comandi: pensize() per impostare la larghezza del tratto della penna e pencolor() per definire il colore.
Una scala disegnata con una penna di spessore 8 e di colore violetto.
Ecco il listato:
"""Disegna un una scala con 3 gradini"""
import turtle
alzata = eval(input("Alzata: "))
pedata = eval(input("Pedata: "))
ninja = turtle.Turtle() # Crea una tartaruga
ninja.pensize(8) # Penna di dimensione 8
ninja.pencolor("violet") # Colore della penna viola, o violetto
ninja.shape("turtle") # Ecco finalmente la tartaruga!
# 1° gradino
ninja.left(90)
ninja.forward(alzata)
ninja.right(90)
ninja.forward(pedata)
# 2° gradino
ninja.left(90)
ninja.forward(alzata)
ninja.right(90)
ninja.forward(pedata)
# 3° gradino
ninja.left(90)
ninja.forward(alzata)
ninja.right(90)
ninja.forward(pedata)
ninja.pencolor("black") # Torno al nero (così la tartaruga si vede meglio)
Come puoi vedere, le istruzioni per la creazione di un gradino sono ripetute 3 volte. Se i gradini fossero 40 il programma sarebbe decisamente troppo lungo e ripetitivo!
Python, come tutti i linguaggi di programmazione completi, può automatizzare una operazione da ripetersi identica molte volte, attraverso una procedura chiamata ciclo. Lo studio della quale lascio come esercizio al lettore: come sostituire quelle tre istruzioni con una sola, un ciclo da eseguirsi tre volte? O quaranta? O mille, per una scala da grattacielo?
L’articolo si basa sul capitolo 5 di Imparare a programmare con Python.