[Pubblichiamo un estratto da Data Science, libro per programmatori che si avvicinano alla scienza dei dati per unire la loro competenza a quelle di matematica e analisi del business e così ricavare informazione da dati eterogenei].
Correlazione oppure causalità?
Penso che non mi sarebbe stato permesso di scrivere questo libro senza una doverosa trattazione delle differenze fra correlazione e causalità. Per questo esempio, userò dati del consumo di TV e delle prestazioni lavorative [scaricabili gratuitamente e compresi nel codice di elaborazione].
La correlazione è una metrica quantitativa compresa fra -1 e 1 che misura come si spostano due variabili l’una rispetto all’altra. Se due variabili hanno una correlazione vicina a -1, significa che quando una variabile cresce, l’altra decresce, e se due variabili hanno una correlazione vicina a +1, questo significa che queste variabili si muovono insieme nella stessa direzione: se una cresce, così fa anche l’altra, e viceversa.
La causalità è l’idea che una variabile influenzi un’altra.
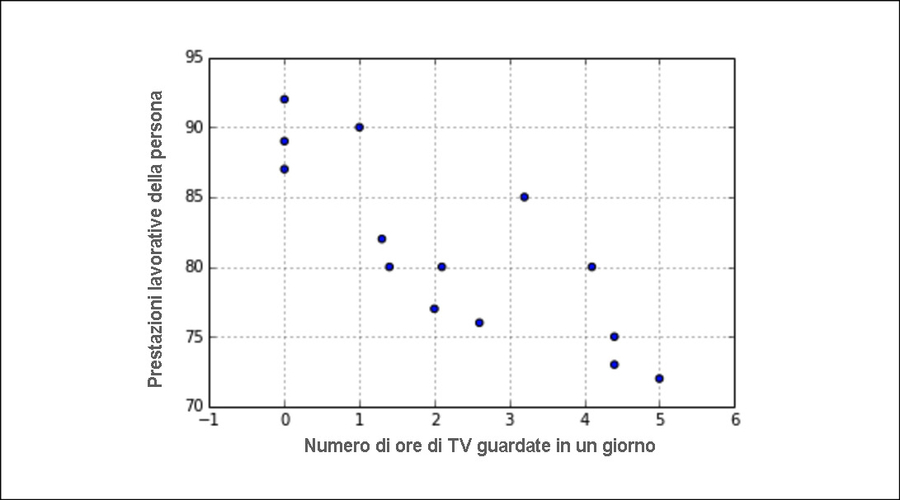
Per esempio, possiamo osservare due variabili: il numero medio di ore passate quotidianamente davanti alla TV e le prestazioni lavorative su una scala da 0 a 100 (0 = prestazioni molto scarse e 100 = prestazioni eccellenti). Ci si potrebbe aspettare che questi due fattori presentino una correlazione negativa: che aumentando il numero di ore quotidiane di TV, calino le prestazioni lavorative medie. Riutilizziamo codice precedente già usato nel libro, con il seguente aspetto:
import pandas as pd
hours_tv_watched = [0, 0, 0, 1, 1.3, 1.4, 2, 2.1, 2.6, 3.2, 4.1, 4.4, 4.4, 5]
Qui, osserviamo sempre lo stesso campione di 14 persone e le loro risposte alla domanda su quante ore di TV guardano in media al giorno (la sera):
work_performance = [87, 89, 92, 90, 82, 80, 77, 80, 76, 85, 80, 75, 73, 72]
Queste sono sempre le stesse 14 persone menzionate in precedenza, nello stesso ordine, ma ora, invece delle ore di TV, abbiamo le loro prestazioni lavorative valutate dall’azienda o da un sistema indipendente:
df = pd.DataFrame({'hours_tv_watched':hours_tv_watched,¬
'work_performance':work_performance})
In precedenza, abbiamo visto – e rivedremo tra poco – un grafico a dispersione di queste due variabili, il quale sembrava mostrare chiaramente un trend verso il basso delle variabili: con un maggiore consumo di ore alla TV, le prestazioni lavorative sembravano calare.
Tuttavia, un coefficiente di correlazione, un numero compreso fra -1 e 1, è un ottimo modo per identificare le relazioni fra le variabili e, contemporaneamente, per quantificarle e valutarne l’intensità.
Ora possiamo introdurre una nuova riga di codice, che ci mostra la correlazione fra queste due variabili:
df.corr() # -0.824
Come abbiamo detto, una correlazione vicina a -1 implica una forte correlazione negativa, mentre una correlazione vicina a +1 implica una forte correlazione positiva.
Questo numero aiuta a supportare l’ipotesi, perché un coefficiente di correlazione prossimo a -1 implica non solo una correlazione negativa, ma anche una intensa correlazione. Di nuovo, possiamo vederlo tramite un grafico a dispersione fra le due variabili. Pertanto, abbiamo dati visuali e dati numerici perfettamente allineati. Questo è un concetto importante, che probabilmente rafforzerà i risultati, quando li comunicherete. Se i numeri e i grafici non concordano, difficilmente la vostra analisi verrà presa seriamente.
Più si guarda televisione, peggio si lavora: un rapporto di correlazione o causalità?
Non potrò mai ribadire a sufficienza che correlazione e causalità sono due concetti distinti. La correlazione quantifica semplicemente il grado con il quale le variabili cambiano insieme, mentre la causalità è l’idea che una variabile determini effettivamente il valore di un’altra. Se volete condividere i risultati delle vostre ricerche in termini di correlazione, potreste forse trovare nel vostro pubblico qualcuno convinto che quel dato vada approfondito. Ma la cosa peggiore è che nessuno potrebbe accorgersi che l’analisi è incompleta e potrebbe prendere decisioni sulla base di una semplice correlazione.
Molto spesso capita che due variabili siano, sì, correlate, ma senza alcuna relazione di causalità fra di esse. I motivi possono essere vari. Eccone alcuni.
- Potrebbe entrare in gioco un fattore di confusione. Questo significa che esiste “in agguato” una terza variabile non individuata e che funge da collegamento fra le due variabili. Per esempio, in precedenza abbiamo visto che si poteva trovare una correlazione negativa fra le ore di TV quotidiane e le prestazioni lavorative: aumentando il numero di ore trascorse davanti alla TV, le prestazioni lavorative potevano decrescere. Questa è una correlazione. Non sembra suggerire proprio che le ore trascorse davanti alla TV causino una riduzione della qualità delle prestazioni lavorative. È più plausibile che suggerisca l’esistenza di un terzo fattore, magari le ore di sonno, in grado di rispondere a questa domanda. Probabilmente, guardando più TV la sera decresce la quantità di ore dedicate al sonno, il che a sua volta limita le prestazioni lavorative. In questo caso il fattore di confusione è rappresentato dal numero di ore di sonno per notte.
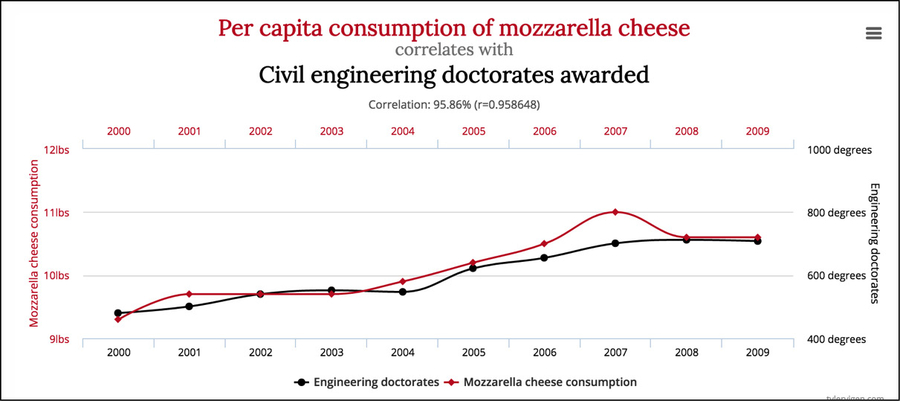
- Le variabili potrebbero non avere proprio nulla a che fare l’una con l’altra! Il tutto potrebbe essere semplicemente frutto di coincidenza. Vi sono molte variabili che sono correlate ma senza alcuna relazione di causalità. Considerate il seguente esempio.
I due andamenti sono molto simili, eppure non esiste un legame causale tra essi.
È molto più probabile che queste due variabili siano semplicemente correlate (aggiungerei che sono correlate più fortemente rispetto all’esempio precedente) piuttosto che il consumo di mozzarelle determini il numero di lauree in ingegneria civile a livello mondiale.
Probabilmente avete già sentito l’affermazione che la correlazione non implica la causalità e quest’ultimo grafico è esattamente il motivo per il quale gli esperti di scienza dei dati devono sempre ricordarlo. Solo perché esiste una correlazione matematica fra le variabili non significa che fra di esse vi sia una relazione di causalità. Fra di esse potrebbero esservi dei fattori di confusione o potrebbero non avere proprio nulla a che fare l’una con l’altra!
Vediamo cosa accade quando ignoriamo le variabili di confusione e le correlazioni finiscono per diventare estremamente fuorvianti.
Il paradosso di Simpson
Il paradosso di Simpson è il motivo formale per cui dovremmo prendere molto seriamente le variabili di confusione. Il paradosso stabilisce che una correlazione fra due variabili può essere completamente invertita considerando fattori differenti. Questo significa che anche se un grafico potrebbe mostrare una correlazione positiva, queste variabili possono diventare anti-correlate prendendo in considerazione un altro fattore (probabilmente un fattore di confusione). Questo può essere un bel problema per gli esperti di statistica.
Supponete di voler esplorare la relazione esistente fra due diverse pagine splash. Chiameremo queste pagine Pagina A e Pagina B. Abbiamo due pagine splash che vorremmo confrontare fra loro e la nostra metrica saranno i tassi di conversione.
Supponete di eseguire un test preliminare e di rilevare i seguenti risultati in termini di conversione.
| Pagina A | Pagina B |
|---|---|
| 75% (263/350) | 83% (248/300) |
Questo significa che la Pagina B ha un tasso di conversione superiore del 10 percento rispetto alla Pagina A. Pertanto, di primo acchito, sembra che la Pagina B rappresenti la scelta migliore, avendo un tasso di conversione superiore. Se dovessimo comunicare questi dati ai nostri colleghi, sembreremmo essere nel giusto!
Tuttavia, vediamo cosa accade tenendo in considerazione la posizione geografica dell’utente.
| Pagina A | Pagina B | |
|---|---|---|
| Costa occidentale | 95% (76 / 80) | 93% (231/250) |
| Costa orientale | 72% (193/270) | 34% (17/50) |
| Entrambe | 75% (263/350) | 83% (248/300) |
Ecco il paradosso! Suddividendo il campione per area geografica, sembra che la Pagina A sia migliore in entrambe le categorie ma peggiore in generale. Questa è la natura meravigliosa e terribile del paradosso. Questo si verifica per via dello sbilanciamento delle classi fra i quattro gruppi.
Il gruppo Pagina A/Costa orientale, così come il gruppo Pagina B/Costa occidentale, forniscono la maggior parte delle persone del campione, alterando i risultati in modo imprevisto. La variabile di confusione, qui, potrebbe essere il fatto che le pagine sono state presentate a ore del giorno differenti e così gli utenti della Costa occidentale hanno gradito di più la Pagina B, mentre quelli della Costa orientale hanno gradito di più la Pagina A.
Esiste una soluzione (e pertanto una risposta) al paradosso di Simpson: la dimostrazione si basa su un complesso sistema di reti bayesiane e va ben oltre gli scopi di questo libro.
La “morale” del paradosso di Simpson è che non dovremmo attribuire una causalità inesistente a due variabili correlate. Potrebbero esservi variabili di confusione ancora da esaminare. Pertanto, se siete in grado di rivelare una correlazione fra due variabili (come l’aspetto del sito web e il tasso di adesione o il consumo di TV e le prestazioni lavorative), dovete assolutamente tentare di isolare quante più variabili possibili che potrebbero essere il vero motivo della correlazione o che almeno siano in grado di spiegare la situazione.
Allora che significa la correlazione?
Come esperto di scienza dei dati, spesso trovo frustrante trovare correlazioni e non essere in grado di individuare una causalità. Il modo migliore e più corretto per ottenere la causalità passa, normalmente, attraverso degli esperimenti casuali. Occorre suddividere la popolazione in gruppi campionati casualmente e svolgere una verifica delle ipotesi per concludere, con un certo grado di sicurezza, che esiste una vera causalità fra le variabili.