Statistiche su Python

[Pubblichiamo un estratto da Data Science con Python, che introduce all’uso di uno dei linguaggi più diffusi nel mondo accademico e professionale per effettuare elaborazioni numeriche arbitrariamente raffinate.]

Il supporto di Python per i numeri casuali e la statistica è suddiviso su più moduli: statistics, numpy.random, pandas e scipy.stats.

Generazione di numeri casuali

Il modulo numpy.random offre dei generatori di numeri casuali per tutte le principali distribuzioni di probabilità.

Il codice di analisi dei dati dovrebbe essere riproducibile: chiunque dovrebbe essere in grado di lanciare lo stesso programma con gli stessi dati di input e ottenere gli stessi risultati. Basta avere l’accortezza di inizializzare sempre il seme pseudo-casuale con la funzione seed(). Altrimenti, i generatori produrranno a ogni esecuzione del programma sequenze pseudo-casuali differenti, e in tal caso sarebbe difficile, se non addirittura impossibile, ottenere gli stessi risultati.

import numpy.random as rnd 
rnd.seed(z)

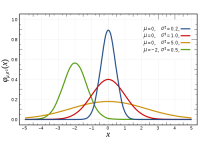
Le seguenti funzioni generano numeri casuali interi e reali a distribuzione uniforme, normale e binomiale. Tutte restituiscono un array numpy avente una certa forma (shape) o determinate dimensioni (size), dove shape è una lista di dimensioni), a meno che il parametro size sia None.

rnd.uniform(low=0.0, high=1.0, size=None) 
rnd.rand(shape)      # Equivale a uniform(Q.Q, 1.0, None) 
rnd.randint(low, high=None, size=None) 
rnd.normal(loc=0.0, scale=1.0, size=None) 
rnd.randn(shape)     # Equivale a normal(0.0, 1.0, shape) 

rnd.binomial(n, p, size=None)

La distribuzione binomiale è essenziale quando occorre configurare un esperimento predittivo e suddividere i dati in un set di addestramento e un set di collaudo. Supponiamo che le dimensioni relative del set di addestramento siano p e quelle del set di collaudo 1 – p. Potete preparare una sequenza binomiale, convertirla in una sequenza booleana di valori True e False e selezionare entrambi gli insiemi da un frame pandas:

selection = rnd.binomial(1, p, size=len(dati)).astype(bool) 
training = df[selection] 
testing = df[-selection]

Calcolo delle misurazioni statistiche

Per offrire una soluzione rapida, il modulo statistics offre le funzioni mean() e stdev().

I frame e le serie pandas contengono delle funzioni per calcolare le correlazioni e le covarianze rispetto ad altri frame o serie, ma anche per calcolare tutte le correlazioni e covarianze a coppie fra le colonne del frame (ma non i valori p) e altre misurazioni statistiche.

Per esplorare le operazioni statistiche supportate da pandas, utilizziamo il rapporto NIAAA sull’alcolismo negli Stati Uniti. Prepariamo due serie e poi calcoliamo la loro correlazione, la covarianza e la skewness:

beer_seriesNY = aco.ix['New York']['Beer'] 
beer_seriesCA = alco.ix['California']['Beer']

beer_seriesNY.corr(beer_seriesCA)

→ 0.97097785391654789

beer_seriesCA.cov(beer_seriesNY)

→ 0.017438162878787872

[x.skew() for x in (beer_seriesCA, beer_seriesNY)]

→ [0.16457291293004678, 0.32838100586347024]

Possiamo applicare le stesse funzioni anche ai frame:

frameNY = alco.ix['New York']

frameNY.skew()

→ Beer 0.328381
→ Wine 0.127308
→ Spirits 0.656699
→ dtype: float64

frameNY.corr() # tutte le correlazioni a coppie

→  Beer Wine Spirits
→ Beer 1.000000 0.470690 0.908969
→ Wine 0.470690 1.000000 0.611923
→ Spirits 0.908969 0.611923 1.000000

frameNY.cov() # tutte le covarianze a coppie

→  Beer Wine Spirits
→ Beer 0.016103 0.002872 0.026020
→ Wine 0.002872 0.002312 0.006638
→ Spirits 0.026020 0.006638 0.050888

Le ultime due funzioni restituiscono un frame di tutte le correlazioni o covarianze a coppie.

Possiamo anche calcolare le correlazioni fra una serie e un frame o fra un frame e un altro frame. Per esempio, controlliamo se esiste una correlazione fra il consumo di alcol e la popolazione nello Stato di New York usando i dati del Census Bureau USA nel periodo compreso fra il 2000 e il 2009:

# Rimuove le ultime due righe: conterranno le stime future 
pop_seriesNY = pop.ix["New York"][:-2]

# Converte l'indice da una data a un intero (l'anno)
pop_seriesNY.index = pop_seriesNY.index.str.split().str[-1].astype(int) 
frameNY.ix[2000:2009].corrwith(pop_seriesNY)

→ Beer -0.520878
→ Wine 0.936026
→ Spirits 0.957697
→ dtype: float64

Notate che le righe nel frame e nella serie sono disposte in ordine inverso. Pandas, però, è sufficientemente intelligente da usare gli indici di riga per individuare le righe corrette. Si tratta, naturalmente, del meccanismo di allineamento dei dati in azione.

Per stimare la significatività della correlazione, usate la funzione pearsonr() del modulo scipy.stats. Questa funzione restituisce sia la correlazione sia il valore-p. Tuttavia, non si integra con i frame pandas e non supporta l’indicizzazione, pertanto sarà vostro compito allineare gli indici e convertire il risultato di nuovo in un frame.

from scipy.stats import pearsonr
# Allinea manualmente gli indici 
pop_sorted = pop_seriesNY.sort_index() 
alco_10 = alco.ix['New York'][-10:]

# Manipola le liste per calcolare tutte le correlazioni e i valori p 
corrs = [(bev,) + pearsonr(alco_10[bev], pop_sorted)
         for bev in alco_10.columns]
# Converte la lista in un frame
pd.DataFrame(corrs, columns=("bev", "r", "p-value")).set_index("bev") 

→  r p-value
→ bev
→ Beer -0.520878 0.122646
→ Wine 0.936026 0.000068
→ Spirits 0.957697 0.000013

Vale la pena di notare che il valore-p per la correlazione beer è eccezionalmente alto. Dovremmo concludere che è improbabile che esista una relazione lineare fra la numerosità della popolazione e il consumo di birra.

Abbiamo dunque immaginato che nel 2009, i consumi di birra e vino potessero essere linearmente indipendenti. La correlazione di Pearson conferma appieno questa ipotesi:

alco2009.corr()

→  Beer Wine Spirits
→ Beer 1.000000 -0.031560 0.452279
→ Wine -0.031560 1.000000 0.599791
→ Spirits 0.452279 0.599791 1.000000

Il valore-p molto elevato della correlazione rappresenta il colpo di grazia per l’ipotesi alternativa:

pearsonr(alco2009["Wine"], alco2009["Beer"])

→ (-0.031560488300856844, 0.82598481310787297)

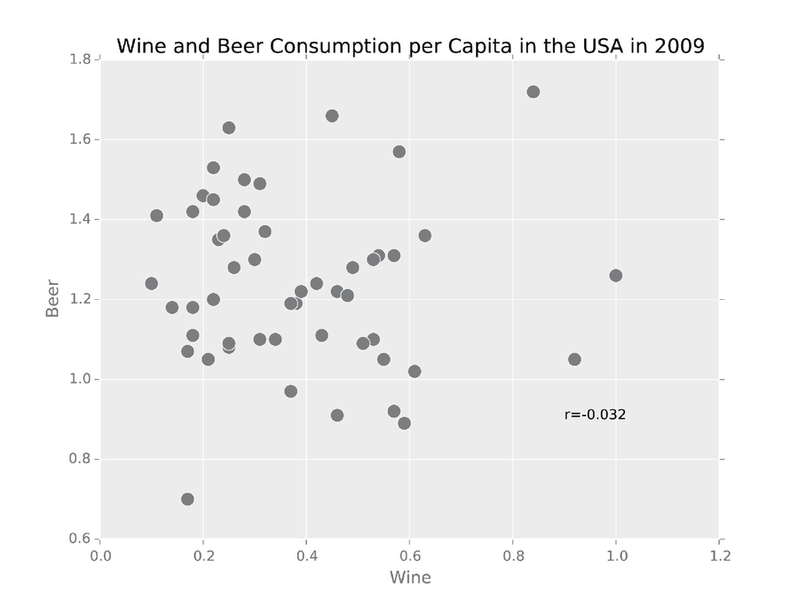
E il seguente grafico a dispersione spiega il perché: i punti sono del tutto dispersi nello spazio, senza alcun particolare allineamento o schema.

Consumo pro capite di vino e birra negli Stati Uniti nel 2009.

Esercitazioni

Chiamare il capitolo da cui tratto questo articolo Probabilità e statistica è stato soprattutto un atto di sconsiderata spavalderia. Ci vorrebbe un intero volume, non poche pagine, anche solo per introdurre la teoria delle probabilità e poi un altro volume per trattare la statistica. Se questo è il vostro primo incontro con queste discipline e intendete davvero diventare esperti di scienza dei dati, preparatevi a studiare, e anche molto. In ogni caso, proviamo a svolgere alcuni progetti interessanti. E che Python sia sempre con voi…

S&P 500 nel XXI secolo (∗)

Scrivete un programma che esegua alcune semplici misurazioni statistiche dei valori di chiusura del pacchetto di azioni S&P 500: media, deviazione standard, skewness e correlazione fra i valori di chiusura e il volume degli scambi nel ventunesimo secolo. La correlazione è affidabile? Potete scaricare i dati storici da Yahoo! Finance. Ricordate che il Ventunesimo secolo è iniziato il 1 gennaio 2001.

Nutrienti in Rete (∗∗∗)

Il database dei nutrienti dello United States Department of Agriculture (USDA)) contiene informazioni relative a circa 9000 cibi e 150 nutrienti. Supponiamo che due nutrienti siano simili se la loro quantità in tutti i cibi sono fortemente e stabilmente correlati: la correlazione è maggiore di 0.7 e il valore-p è minore di 0.01. Scrivete un programma che utilizzi i dati del file NUT_data.txt per costruire una rete di nutrienti simili. Ogni nutriente della rete forma un nodo e due nodi sono connessi se due nutrienti sono simili.

La rete presenta una qualsiasi struttura comunitaria? In caso affermativo, quali nutrienti stanno insieme?

L’ingresso più facile in un campo molto complesso.